Трение во вращательных парах

Вращательная кинематическая пара образуется цапфой (опорной частью вала) и охватывающим её подшипником.

Для того чтобы цапфа, находящаяся под действием нескольких приложенных к ней сил, могла вращаться, необходимо, чтобы равнодействующая Р этих сил (рис. 16.10) создавала момент не меньший момента силы трения.

Рис. 16.10

Разложив силу Р на нормальную Рⁿ и тангенциальную Р ^t составляющие и обозначив через: r плечо действия силы Р относительно оси вращения цапфы; R – радиус цапфы; l - угол между линией действия силы Р и радиусом, проведённым в точку приложения силы P, получим:

момент, вращающий цапфу, равен

;

момент силы F трения равен

.

Для возможности движения необходимо соблюдение условия

,

откуда

,

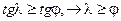и поэтому

.

Следовательно, момент силы Р не может вращать цапфы, если линия действия силы Р проходит внутри круга с радиусом .

Такой круг получил название – круга трения.

Трение в пятах (трение верчения)

Трение в пятах имеет место на поверхности соприкосновения двух прижатых одно к другому тел, вращающихся одно относительно другого вокруг нормали к поверхности соприкосновения (рис. 16.11, а).

Рис. 16.11

При учете сопротивления, оказываемого силами трения моменту, вращающему одно тело относительно другого, приходится определять равнодействующий момент сил трения, заменяя элементарные силы трения на всей поверхности трения равнодействующей силой, приложенной на окружности с радиусом R. Определим величину радиуса R, предположив, что поверхность трения представляет собой кольцевую площадь с внешним радиусом r ₁ и внутренним радиусом r ₂ и что вращение происходит вокруг общего центра окружностей (рис. 16.11, б).

Полная сила трения скольжения равна:

,

где р – давление на поверхности трения, т.е. сила, приходящаяся на единицу поверхности трения; - площадь поверхности соприкосновения.

Момент полной силы трения

,

где R – радиус окружности, на которой приложена равнодействующая элементарных сил трения.

Элементарная сила трения, распределённая по кольцу с площадью , равна

.

Момент элементарной силы трения равен

.

Суммарный момент

.

Тогда приравнивая правые половины уравнений, получаем равенство

,

откуда

.

При r ₂ = 0, получаем .

Контрольные вопросы

44. Что такое трение, и от чего оно зависит.

45. Трение скольжения: сила, угол и конус трения.

46. Трение на горизонтальной плоскости.

47. Трение на наклонной плоскости.

48. Трение клинчатого ползуна, приведенный коэффициент трения.

49. Трение во вращательных парах.

50. Трение в пятах.

Лекция 17

Трение гибких тел. Трение качения. Коэффициент полезного действия механизмов: общие сведения, КПД при последовательном и параллельном соединении звеньев, КПД винтовой передачи.