 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Трение на наклонной плоскости
|
|
Рассмотрим случай, когда на тело, находящееся на наклонной плоскости с углом l к горизонту, действует одна сила, перпендикулярная основанию плоскости (рис 16.5), например сила веса.

Рис. 16.5
В этом случае возможно движение только вниз при соблюдении условия  . При
. При  под действием силы, перпендикулярной основанию плоскости, движение, независимо от величины силы, не может ни возникнуть, ни продолжаться без замедления.
под действием силы, перпендикулярной основанию плоскости, движение, независимо от величины силы, не может ни возникнуть, ни продолжаться без замедления.
Плоскость с углом наклона, меньшим угла трения, называется самотормозящей.
Рассмотрим случай, когда на тело, находящееся на плоскости, наклоненной под углом l к горизонту, действуют две силы, одна из которых перпендикулярна основанию плоскости, а другая параллельна. В этом случае возможно движение тела вверх, или вниз по наклонной плоскости.
1. Движение тела вверх по наклонной плоскости (рис. 16.6).

Рис. 16.6
В этом случае параллельная основанию плоскости сила Р должна быть направлена вправо. Для возможности движения вверх по плоскости необходимо, чтобы равнодействующая R сил P и Q составляла угол b с перпендикуляром к плоскости не меньше угла трения j, т.е. необходимо выполнение условия
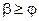 .
.
Из построения следует
 .
.
Из приведенных выше неравенства и равенства вытекает следующее условие для возможности движения тела вверх по наклонной плоскости:
 .
.
2. Движение тела вниз по наклонной плоскости (рис. 16.7).
В этом случае из построения следует

и, следовательно, движения тела вниз по наклонной плоскости оказывается при 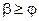 возможным при соблюдении условия
возможным при соблюдении условия
 .
.

Рис. 16.7
На рис. 16.7 сила Р направлена вправо и является силой, противодействующей движению. Необходимость в силе Р, направленной влево (рис. 16.8), для движения тела вниз будет только в том случае, если под действием только одной силы Q движение не будет происходить (самотормозящая плоскость).
Из построения (рис. 16.8) получаем

При 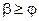 необходимая для движения сила Р должна удовлетворять условию
необходимая для движения сила Р должна удовлетворять условию
 .
.

Рис. 16.8
Дата публикования: 2015-11-01; Прочитано: 509 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
