Трение на горизонтальной плоскости

Движение тела на плоскости можно рассматривать под действием только одной силы, т.к. несколько действующих сил на тело можно привести к одной - равнодействующей.

Предположим, что на тело действует сила Р (рис. 16.4) под углом l к нормали. Перенесём силу Р в точку пересечения её вектора с перпендикуляром к плоскости соприкосновения и разложим её по двум взаимно перпендикулярным направлениям. Нормальная составляющая Рⁿ, прижимая тело к плоскости, создает противодействующую движению тела силу F ₀ трения покоя; тангенциальная составляющая Р ^t стремится сдвинуть тело.

Рис. 16.4

Для возможности движения необходимо выполнение условия:

.

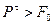Так как

То

,

откуда

,

где j₀ - угол трения покоя.

Из этого следует, что сила, действующая внутри конуса трения, независимо от её величины, привести в движение тело не может.

Подставив в приведённые выше неравенства F вместо F ₀, f и j вместо f ₀ и j₀ и заменив во всех неравенствах знак > знаками ³, придём к заключению, что движение тела на плоскости возможно лишь при соблюдении условия .

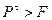При получаем и движение с постоянной скоростью, при получаем и движение с ускорением.

При возникновение движения невозможно, при вызванное какими-либо силами и продолжающееся по инерции движение тела при действии на него силы Р будет происходить с замедлением, так как в этом случае создаваемая силой Рⁿ противодействующая движению сила трения будет больше силы Р ^t, поддерживающей движение.