Правило Лопиталя

Другой способ раскрытия неопределенностей типа 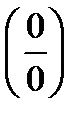или 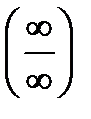доставляет так называемое правило Лопиталя, к изложению которого мы переходим.

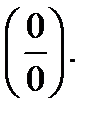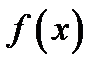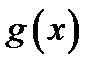Теорема Лопиталя Пусть функции и в некоторой проколотой окрестности 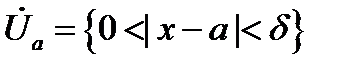удовлетворяют требованиям:

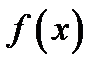и 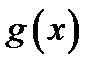непрерывны и дифференцируемы в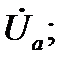

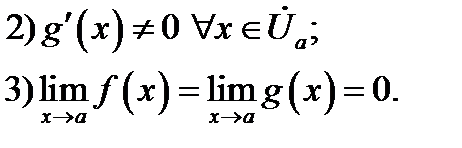
Если при этом существует(конечный или бесконечный) предел отношения производных: 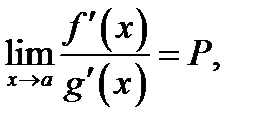то и существует равный ему предел отношения самих функций: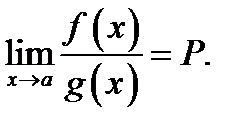

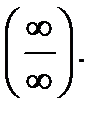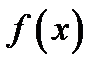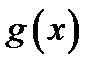Теорема Лопиталя Пусть функции и в некоторой проколотой окрестности 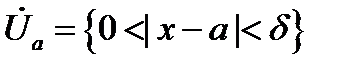удовлетворяют требованиям:

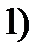
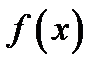и 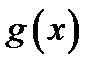непрерывны и дифференцируемы в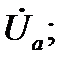

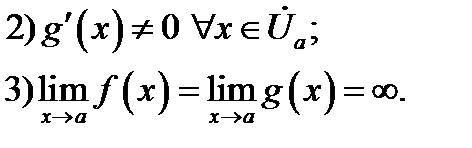
Если при этом существует (конечный или бесконечный) предел отношения производных: 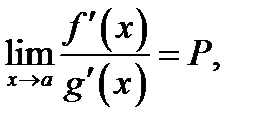то и существует равный ему предел отношения самих функций: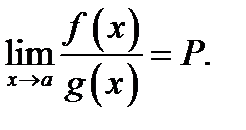

Например, для рассмотренного выше предела имеем

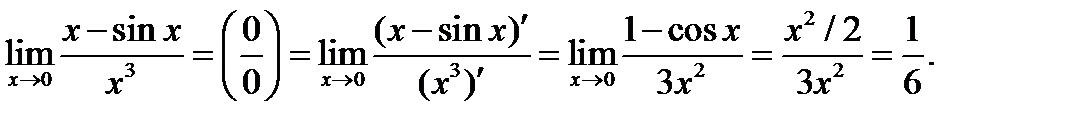
Лекция 4. Свойства функций, непрерывных на отрезке: ограниченность, достижение наибольшего и наименьшего значений, реализация всех промежуточных значений. Свойства дифференцируемой функции: монотонность, экстремумы. Схема построения графика функции с помощью первой производной