Угол между двумя плоскостями

А₁х+В₁y-C₁z+D₁ =0 и А₂х+В₂y-C₂z+D₂ =0 определяется по формуле

Условие перпендикулярности двух плоскостей имеет вид:

= 0

Условие параллельности двух плоскостей имеет вид:

Расстояние от точки N (х₁,у₁, z₁) до плоскости Ax + By + Сz + D = 0 определяется по формуле

d =

Уравнение плоскости, проходящей через три данные точки A (х₁,у₁, z₁), B(х₂,у₂, z₂), C(х₃,у₃, z₃). имеет вид

Прямая линия в пространстве.

Канонические уравнения прямой линии в пространстве, или уравнения прямой с направляющими коэффициентами, имеют вид

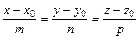
где х₀,у₀, z₀ - координаты точки, через которую проходит пря­мая, а т, п и р -направляющие коэффициенты прямой, кото­рые являются проекциями на координатные оси Ох, Оу, Оz на­правляющего вектора прямой.

Если α, β и γ - углы между прямой и координатными осями Ох, Оу и Оz, то

cos а = ± ; cos β = ± 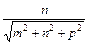; cos γ = ± ;

называются направляющими косинусами пря­мой. Направляющие коэффициенты т, п и р можно рассматри­вать как проекции на координатные оси вектора, параллельного прямой, причем т, п и р не могут быть одновременно равны нулю.

В параметрическом виде уравнения прямой линии в про­странств е записываются так:

x =x₀ + mt; y =y₀ + nt; z =z₀ + pt

где t — параметр.

Общие уравнения прямой в пространстве:

Каждое из уравнений - уравнение плоскости, и таким образом прямая в пространстве может рассматриваться как пере­сечение двух плоскостей, причем плоскости эти предполагаются непараллельными, т. е. соотношение

не имеет места.

Условие параллельности двух прямых в пространстве:

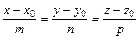
имеет вид

Условие перпендикулярности этих двух прямых имеет вид

mm₁ + nn₁ + pp₁ = 0

Угол между двумя прямыми определяется по фор­муле

Уравнения прямой, проходящей через две данныеточкиA (х₁,у₁, z₁), B(х₂,у₂, z₂) запишутся в виде

Плоскость и прямая