Системы линейных уравнений. Матричный метод решения систем линейных уравнений ( с помощью обратной матрицы). Пример

В этой статье поговорим о матричном методе решения систем линейных алгебраических уравнений вида 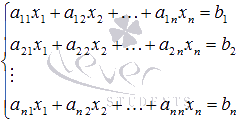, которые в матричной форме записываются как 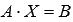, где 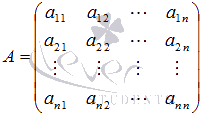- основная матрица системы, 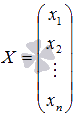- матрица-столбец неизвестных переменных, 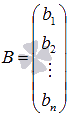- матрица свободных членов.

Сначала опишем суть матричного метода, остановимся на условии применимости этого метода, далее подробно разберем решения нескольких примеров.

Сразу оговоримся, что решение систем линейных алгебраических уравнений матричным методом и решение СЛАУ с помощью обратной матрицы есть одно и то же. Поэтому рекомендуем освежить в памяти теорию раздела обратная матрица: определение, свойства, методы нахождения.

Найдите решение системы линейных алгебраических уравнений 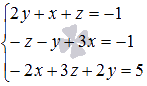с помощью обратной матрицы.

Упорядочив неизвестные переменные в уравнениях системы, запишем ее в матичной форме 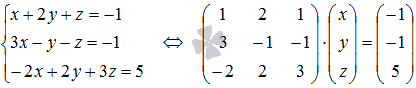. Вычислим определитель основной матрицы:

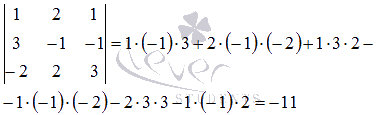
Он отличен от нуля, поэтому решение системы уравнений может быть найдено с помощью обратной матрицы как 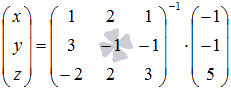. Найдем обратную матрицу по формуле :

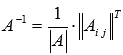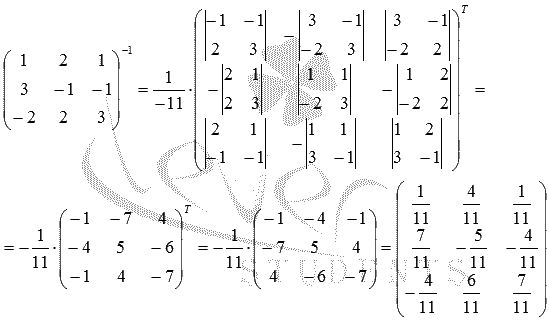
Получим искомое решение: