	Главная \| Случайная страница \| Контакты \| Мы поможем в написании вашей работы!

Решите самостоятельно следующие задачи. 1. Полагая, что между переменными Х и У существует корреляционная зависимость: а) определить выборочный коэффициент корреляции

⇐ Предыдущая 13 14 15 16 17 18 19 20 2122

1. Полагая, что между переменными Х и У существует корреляционная зависимость: а) определить выборочный коэффициент корреляции, сделать вывод о тесноте и направлении связи; б) найти уравнение прямой регрессии У на Х; в) построить по полученному уравнению прямую регрессии.

1.1.

у	Х
						∑
			-	-	-	-
	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
∑							∑=100

1.2.

у	Х
						∑
			-	-	-	-
	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
∑							∑=100

1.3.

у	Х
						∑
			-	-	-	-
	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
∑							∑=100

1.4.

у	Х
						∑
			-	-	-	-
	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
∑							∑=100

1.5.

у	Х
						∑
			-	-	-	-
	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
∑							∑=100

1.6.

у	Х
						∑
			-	-	-	-
	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
∑							∑=100

1.7.

у	Х
						∑
			-	-	-	-
	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
∑							∑=100

1.8.

у	Х
						∑
			-	-	-	-
	-			-	-	-
	-	-				-
	-	-				-
	-	-	-
∑							∑=100

1.9.

у	Х
						∑
			-	-	-	-
					-	-
	-				-	-
	-	-	-
	-	-	-
∑							∑=100

1.10.

у	Х
165-170	170-175	175-180	180-185	185-190	190-195	∑
60-70				-	-	-
70-80					-	-
80-90					-	-
90-100	-					-
100-110	-	-	-	-
∑							∑=250

1.11.

у	Х
0-2	2-4	4-6	6-8	8-10	10-12	∑
6-8					-	-
8-10					-	-
10-12	-
12-14	-	-
14-16	-			-
∑							∑=100

1.12.

у	Х
0,4-0,8	0,8-1,2	1,2-1,6	1,6-2,0	2,0-2,4	2,4-2,8	∑
7-9			-	-	-	-
9-11	-				-	-
11-13	-	-				-
13-15	-	-				-
15-17	-	-	-
∑							∑=100

1.13.

у	Х
19,5	20,0	20,5	21,0	21,5	22,0	∑
9,6			-	-	-	-
9,8					-	-
10,0	-					-
10,2	-	-
∑							∑=50

1.14.

У	Х
5-9	9-13	13-17	17-21	21-25	25-29	∑
1-3	-	-	-	-
3-5	-	-	-
5-7	-	-				-
7-9	-				-	-
9-11	-			-	-	-
11-13			-	-	-	-
13-15		-	-	-	-	-
∑							∑=50

1.15.

У	Х
						∑
	-	-	-		-
	-	-
	-	-
	-					-
	-			-	-	-
			-	-	-	-
		-	-	-	-	-
∑							∑=100

1.16.

У	Х
1,25	1,5	1,75		2,25	∑
	-	-
	-	-
	-				-
				-	-
			-	-	-
∑						∑=50

1.17.

У	Х
	2,5		3,5		∑
	-	-	-
	-	-
	-				-
					-
			-	-	-
∑						∑=50

1.18.

У	Х
					∑
			-	-	-
	-				-
	-
	-	-
	-	-	-
∑						∑=200

1.19.

У	Х
					∑
			-	-	-
			-	-	-
	-				-
	-
	-	-
∑						∑=200

1.20.

У	Х
6,0-7,5	7,5-9,0	9,0-10,5	10,5-12,0	12,0-13,5	∑
16-18		-	-	-	-
18-20			-	-	-
20-22	-				-
22-24	-	-
24-26	-	-
∑						∑=30

1.21.

У	Х
					∑
8,0	-	-
8,5	-				-
9,0				-	-
9,5				-	-
10,0			-	-	-
∑						∑=100

1.22.

У	Х
10-15	15-20	20-25	25-30	30-35	∑
2,0-2,5	-	-	-	-
2,5-3,0	-	-	-
3,0-3,5	-	-			-
3,5-4,0				-	-
4,0-4,5		-	-	-	-
∑						∑=40

1.23.

У	Х
5-15	15-25	25-35	35-45	45-55	∑
45-55	-	-	-
55-65	-
65-75
75-85				-	-
∑						∑=100

1.24.

У	Х
1-3	3-5	5-7	7-9	9-11	∑
8-9			-	-	-
9-10				-	-
10-11				-	-
11-12	-
12-13	-	-
13-14	-	-	-
∑						∑=100

1.25.

У	Х
50-60	60-70	70-80	80-90	90-100	∑
20-40		-	-	-	-
40-60			-	-	-
60-80	-				-
80-100	-
100-120	-	-
120-140	-	-	-	-
∑						∑=100

1.26.

У	Х
2,5-3,5	3,5-4,5	4,5-5,5	5,5-6,5	6,5-7,5	∑
			-	-	-
					-
	-			-	-
	-				-
	-	-
	-	-
∑						∑=100

1.27.

У	Х
0-2	2-4	4-6	6-8	8-10	10-12	12-14	∑
0-5	-	-	-	-
5-10	-	-
10-15	-
15-20							-
20-25				-	-	-	-
25-30			-	-	-	-	-
∑								∑=50

1.28.

У	Х
							∑
0-12	-	-	-	-
12-24	-	-	-
24-36	-	-					-
36-48	-					-	-
48-60				-	-	-	-
60-72			-	-	-	-	-
∑								∑=100

1.29.

У	Х
							∑
			-	-	-	-	-
					-	-	-
						-	-
	-						-
	-	-
	-	-	-	-
∑								∑=200

1.30.

У	Х
3,5	4,0	4,5	5,0	5,5	6,0	6,5	∑
4,1	-	-	-	-	-		-
4,3	-	-	-
4,5	-	-					-
4,7	-	-					-
4,9	-					-	-
5,1	-					-	-
5,3				-	-	-	-
5,5		-	-	-	-	-	-
∑								∑=100

1.31.

У	Х
4-8	8-12	12-16	16-20	20-24	24-28	28-32	∑
5-10			-	-	-	-	-
10-15					-	-	-
15-20	-					-	-
20-25	-	-				-	-
25-30	-	-	-				-
30-35	-	-	-
35-40	-	-	-	-	-	-
40-45	-	-	-	-	-	-
∑								∑=150

2. Полагая, что между переменными Х и У существует корреляционная зависимость: а) определить выборочный коэффициент корреляции, сделать вывод о тесноте и направлении связи; б) найти уравнение прямой регрессии методом наименьших квадратов; в) построить по полученному уравнению прямую регрессии.

2.1.

x_i
y_i	4,6	5,0	4,1	2,1	2,9

2.2.

x_i
y_i	3,2	4,2	2,7	0,7	1,5

2.3.

x_i
y_i	4,4	5,4	3,9	3,1	5,9

2.4.

x_i
y_i	0,8	0,3	2,3	3,8	2,8

2.5.

Рост
вес

2.6.

Год
стоимость

2.7.

Год
продукция

2.8.

Месяц	март	апрель	май	июнь	июль
прибыль

2.9.

x_i		2,2		4,5	5,1
y_i	0,7	1,6	3,1	3,3	3,5	4,1

2.10.

x_i
y_i	1,3	2,5	0,8	3,8	1,8	3,5

2.11.

x_i
y_i	3,5	10,3	19,8	22,9	24,0	24,5

2.12.

x_i
y_i	3,8	3,4	2,6	2,0	1,7	1,4	1,3

2.13.

x_i		4,1	3,8	3,9	1,2	3,9	4,1	0,8	0,7	1,3
y_i	23,6	31,9	35,2	36,4	23,6	34,0	38,2	17,3	28,8	19,7

2.14.

x_i	3,0	1,1	2,9	3,0	0,8	1,5	2,1	3,2	1,2	3,0
y_i	37,6	18,5	29,1	38,5	18,8	20,6	29,6	36,8	15,8	33,4

2.15.

x_i
y_i

2.16.

x_i
y_i

Таблица 1

Значения функции Ф(х)=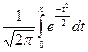

x
0,0	0,0000
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9

x		x		x		x
3,0	0,49865	3,5	0,49977	4,0	0,499968	4,5	0,4999966
3,1	0,49903	3,6	0,49984	4,1	0,499979	4,6	0,4999979
3,2	0,49931	3,7	0,49989	4,2	0,499987	4,7	0,4999987
3,3	0,49952	3,8	0,49993	4,3	0,499991	4,8	0,4999992
3,4	0,49966	3,9	0,49995	4,4	0,499995	4,9	0,4999995

Таблица 2

Критические точки распределения Стьюдента

Число степеней свободы	Уровень значимости α (двусторонняя критическая область)
0,10	0,05	0,02	0,01	0,002	0,001
	6,31 2,92 2,35 2,13 2,01 1,94 1,89 1,86 1,83 1,81 1,80 1,78 1,77 1,76 1,75 1,75 1,74 1,73 1,73 1,73 1,72 1,72 1,71 1,71 1,71 1,71 1,71 1,70 1,70 1,70 1,68 1,67 1,66 1,64	12,7 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 2,23 2,20 2,18 2,16 2,14 2,13 2,12 2,11 2,10 2,09 2,09 2,08 2,07 2,07 2,06 2,06 2,06 2,05 2,05 2,05 2,04 2,02 2,00 1,98 1,96	31,82 6,97 4,54 3,75 3,37 3,14 3,00 2,90 2,82 2,76 2,72 2,68 2,65 2,62 2,60 2,58 2,57 2,55 2,54 2,53 2,52 2,51 2,50 2,49 2,49 2,48 2,47 2,46 2,46 2,46 2,42 2,39 2,36 2,33	63,7 9,92 5,84 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,05 3,01 2,98 2,95 2,92 2,90 2,88 2,86 2,85 2,83 2,82 2,81 2,80 2,79 2,78 2,77 2,76 2,76 2,75 2,70 2,66 2,62 2,58	318,3 22,33 10,22 7,17 5,89 5,21 4,79 4,50 4,30 4,14 4,03 3,93 3,85 3,79 3,73 3,69 3,65 3,61 3,58 3,55 3,53 3,51 3,49 3,47 3,45 3,44 3,42 3,40 3,40 3,39 3,31 3,23 3,17 3,09	637,0 31,6 12,9 8,61 6,86 5,96 5,40 5,04 4,78 4,59 4,44 4,32 4,22 4,14 4,07 4,01 3,96 3,92 3,88 3,85 3,82 3,79 3,77 3,74 3,72 3,71 3,69 3,66 3,66 3,65 3,55 3,46 3,37 3,29
	0,05	0,025	0,01	0,005	0,001	0,0005
Уровень значимости α (односторонняя критическая область)

Таблица 3

Таблица значений q=q(β;n)

n	γ	n	γ
0,95	0,99	0,999	0,95	0,99	0,999
	1,37 1,09 0,92 0,80 0,71 0,65 0,59 0,55 0,52 0,48 0,46 0,44 0,42 0,40 0,39	2,67 2,01 1,62 1,38 1,20 1,08 0,98 0,90 0,83 0,78 0,73 0,70 0,66 0,63 0,60	5,64 3,88 2,98 2,42 2,06 1,80 1,60 1,45 1,33 1,23 1,15 1,07 1,01 0,96 0,92		0,37 0,32 0,28 0,26 0,24 0,22 0,21 0,188 0,174 0,161 0,151 0,143 0,115 0,099 0,089	0,58 0,49 0,43 0,38 0,35 0,32 0,30 0,269 0,245 0,226 0,211 0,198 0,160 0,136 0,120	0,88 0,73 0,63 0,56 0,50 0,46 0,43 0,38 0,34 0,31 0,29 0,27 0,211 0,185 0,162

Таблица 4

Критические точки распределения F Фишера-Снедекора

Уровень значимости α=0,01
k₂	k₁

	98,49 34,12 21,20 16,26 13,74 12,25 11,26 10,56 10,04 9,86 9,33 9,07 8,86 8,68 8,53 8,40	99,01 30,81 18,00 13.27 10,92 9,55 8,65 8,02 7,56 7,20 6,93 6,70 6,51 6,36 6,23 6,11	99,17 26.46 16,69 12,06 9,78 8,45 7,59 6,99 6,55 6,22 5,95 5,74 5,56 5,42 5,29 5,18	99,25 28,71 15,98 11,39 9,15 7,85 7,01 6,42 5,99 5,67 5,41 5,20 5,03 4,89 4,77 4,67	99,30 28,24 15,52 10,97 8,75 7,46 6,63 6,06 5,64 5,32 5,06 4,86 4,69 4,56 4,44 4,34	99,33 27,91 15,21 10,67 8,47 7,19 6,37 5,80 5,39 5,07 4,82 4,62 4,46 4,32 4,20 4,10	99,34 27,67 14,98 10,45 8,26 7,00 6,19 5,62 5,21 4,88 4,65 4,44 4,28 4,14 4,03 3,93	99,36 27,49 14,80 10,27 8,10 6,84 6,03 5,47 5,06 4,74 4,50 4,30 4,14 4,00 3,89 3,79	99,38 27,34 14,66 10,15 7,98 6,71 5,91 5,35 4,95 4,63 4,39 4,19 4,03 3,89 3,78 3,68	99,40 27,23 14,54 10,05 7,87 6,62 5,82 5,26 4,85 4,54 4,30 4,10 3,94 3,80 3,69 3,59	99,41 27,13 14,45 9,96 7,79 6,54 5,74 5,18 4,78 4,46 4,22 4,02 3,86 3,73 3,61 3,52	99,42 27,05 14,37 9,89 7,72 6,47 5,67 5,11 4,71 4,40 4,16 3,96 3,80 3,67 3,55 3,45

Уровень значимости α=0,05
k₂	k₁

	18,51 10,13 7,71 6,61 5,99 5,59 5,32 5,12 4,96 4,84 4,75 4,67 4,60 4,54 4,49 4,45	19,00 9,55 6,94 5,79 5,14 4,74 4,49 4,26 4,10 3,98 3,88 3,80 3,74 3,68 3,63 3,59	19,16 9,28 6,59 5,41 4,76 4,35 4,07 3,86 3,71 3,59 3,49 3,41 3,34 3,29 3,24 3,20	19,25 9,12 6,39 5,19 4,53 4,12 3,84 3,63 4,48 3,36 3,26 3,18 3,11 3,06 3,01 2,96	19,30 9,01 6,26 5,05 4,39 3,97 3,69 3,48 3,33 3,20 3,11 3,02 2,96 2,90 2,85 2,81	19,33 8,94 6,16 4,95 4,28 3,87 3,58 3,37 3,22 3,09 3,00 2,92 2,85 2,79 2,74 2,70	19,36 8,88 6,09 4,88 4,21 3,79 3,50 3,29 3,14 3,01 2,92 2,84 2,77 2,70 2,66 2,62	19,37 8,84 6,04 4,82 4,15 3,73 3,44 3,23 3,07 2,95 2,85 2,77 2,70 2,64 2,59 2,55	19,38 8,81 6,00 4,78 4,10 3,68 3,39 3,18 3,02 2,90 2,80 2,72 2,65 2,59 2,54 2,50	19,39 8,78 5,96 4,74 4,06 3,63 3,34 3,13 2,97 2,86 2,76 2,67 2,60 2,55 2,49 2,45	19,40 8,46 5,93 4,70 4,03 3,60 3,31 3,10 2,94 2,82 2,72 2,63 2,56 2,51 2,45 2,41	19,41 8,74 5,91 4,68 4,00 3,57 3,28 3,07 2,91 2,79 2,69 2,60 2,53 2,48 2,42 2,38

Таблица 5

Критические точки распределения χ²

Число степеней свободы	Уровень значимости α
0,01	0,025	0,05	0,95	0,975	0,89
	6,б 9,2 11,3 13,3 15,1 16,8 18,5 20,1 21,7 23,2 24,7 26,2 27,7 29,1 30,6 32,0 33,4 34,8 36,2 37,6 38,9 40,3 41,6 43,0 44,3 45,6 47,0 48,3 49,6 50,9	5,0 7,4 9,4 11,1 12,8 14,4 16,0 17,5 19,0 20,5 21,9 23,3 24,7 26,1 27,5 28,8 30,2 31,5 32,9 34,2 35,5 36,8 38,1 39,4 40,6 41,9 43,2 44,5 45,7 47,0	3,8 6,0 7,8 9,5 11,1 12,6 14,1 15,5 16,9 18,3 19,7 21,0 22,4 23,7 25,0 26,3 27,6 28,9 30,1 31,4 32,7 33,9 35,2 36,4 37,7 38,9 40,1 41,3 42,6 43,6	0,0039 0,103 0,352 0,711 1,15 1,64 2,17 2,73 3,33 3,94 4,57 5,23 5,89 6,57 7,26 7,96 8,67 9,39 10,1 10,9 11,6 12,3 13,1 13,8 14,6 15,4 16,2 16,9 17,7 18,5	0,00098 0,051 0,2 ⇐ Предыдущая 13 14 15 16 17 18 19 20 2122 Дата публикования: 2015-10-09; Прочитано: 848 \| Нарушение авторского права страницы \| Мы поможем в написании вашей работы! studopedia.org - Студопедия.Орг - 2014-2025 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.007 с)...