Плоскость

На чертеже плоскость отображается в виде проекций:

- трех точек не лежащих на одной прямой линии (рисунок 3.12,а).

- прямой линии и точки, не принадлежащей этой прямой (рисунок 3.12,б).

- двух пересекающихся прямых (рисунок 3.12,в).

- двух параллельных прямых (рисунок 3.12,г).

- плоской фигурой (рисунок 3.13.).

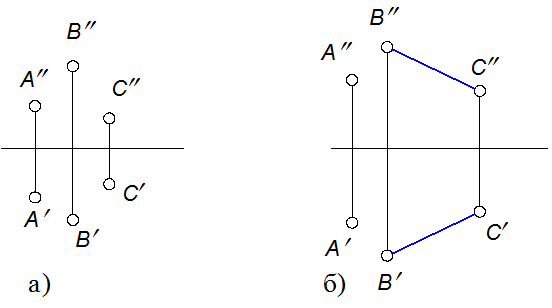
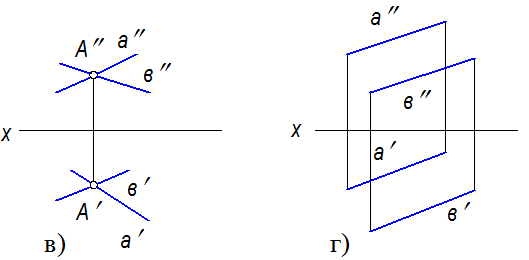
Рисунок 3.12

Различное положение плоскости относительно плоскостей проекций

Плоскость общего положения (не перпендикулярна и не параллельна ни одной плоскости проекций) (рисунки 3.12, 3.13).

Рисунок 3.13

Плоскость частного положения. Плоскость, перпендикулярная горизонтальной плоскости проекций (a ^ p₁, ABC Î a), называется горизонтально проецирующей плоскостью (рисунок 3.14).

Рисунок 3.14

Плоскость перпендикулярная фронтальной плоскости проекций (b^p₂, АВС Î b), называется фронтально проецирующей плоскостью (рисунок 3.15)

Рисунок 3.15

Плоскость перпендикулярная профильной плоскости проекций (g ^ p₃, АВС Î g), называется профильно проецирующей плоскостью (рисунок 3.16).

Рисунок 3.16

Плоскость, параллельная горизонтальной плоскости проекций, - горизонтальная плоскость. Любая геометрическая фигура, принадлежащая этой плоскости, проецируется на p₁ без искажения, а на плоскости p₂ и p₃ проецируется в прямые.

Плоскость, параллельная фронтальной плоскости проекций, называется фронтальной плоскостью.

Плоскость, параллельная профильной плоскости проекций, называется профильной плоскостью.

Главные линии плоскости

Среди прямых линий, которые могут быть расположены в плоскости, особое место занимают три вида прямых.

Горизонтали (h) - прямые, лежащие в плоскости (АВС) и параллельные горизонтальной плоскости проекций(рисунок 3.17). фронтальная проекция горизонтали параллельна оси Ох (h² 2 Ox).

Фронтали (f) - прямые, лежащие в плоскости (АВС) и параллельные фронтальной плоскости, проекций (f Î a, f 2 p₂ f ¢ 2 Ox).

Профильные прямые - прямые, лежащие в данной плоскости и параллельные профильной плоскости проекций.

Рисунок 3.17

Взаимное расположение прямой и плоскости

Возможны три случая:

- прямая принадлежит плоскости;

- прямая параллельна плоскости;

- прямая пересекает плоскость.

Прямая принадлежит плоскости, если две ее точки принадлежат той же плоскости. На рисунке 3.18 (а) плоскость задана пересекающими прямыми n и k. Прямая m принадлежит плоскости, т.к прямая m имеет две общие точки с плоскостью (В и С).

Прямая принадлежит плоскости, если одна ее точка принадлежит плоскости и она параллельна прямой, лежащей в плоскости.

Прямая n принадлежит плоскости (m 2 k), т.к имеет с плоскостью одну общую точку С и параллельна какой либо прямой, расположенной в этой плоскости (n 2 AB), (рисунок 3.19,б).

a) б)

Рисунок 3.18

Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.

Параллельность прямой и плоскости. При решении вопроса о параллельности прямой линии m плоскости необходимо опираться на известное положение стереометрии: прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскости (m || n) (рисунок 3.19)

Рисунок 3.19

Пересечение прямой линии с плоскостью

Для нахождения точки пересечения прямой с плоскостью следует проделать следующие построения (рисунок 3.20):

- через данную прямую a провести проецирующую плоскость w;

- построить проекции линий пересечения 1-2 данной плоскости a и вспомогательной w;

- построить проекции точки К, получающейся в пересечении прямых a и 1-2.

Точка К будет искомой, так как она принадлежит прямой a и плоскости a.

Рисунок 3.20 Рисунок 3.21

На рисунке 3.21 показано нахождение точки встречи прямой a с плоскостью, заданной треугольником ABC, на рисунке 3.22a – с плоскостью, заданной параллельными прямыми b и c, а на рисунке 3.22б – горизонтальным и фронтальным следом.

В первом и третьем случае через прямую a проведена горизонтально проецирующая плоскость w, а во втором – фронтально проецирующая.

Видимость отдельных частей прямой a определена способом конкурирующих точек.

Рис 3.22

Перпендикулярность прямой и плоскости. Перпендикулярные плоскости.

В задачах на построение проекции прямого угла используется теорема: если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая не перпендикулярна ей, то такой угол на эту плоскость проецируется в прямой угол.

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. В качестве пересекающихся прямых чаще всего выбирают горизонталь и фронталь плоскости (рисунок 3.23), так как они проецируются в натуральную величину на соответствующие плоскости проекции (h II p ₁, а f II p₂, а следовательно, h ¢ и f ² – натуральные величины).

Рисунок 3.23

Прямая перпендикулярна плоскости, когда горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция – фронтальной проекции фронтали этой плоскости (a ¢ ^ h ¢, a² ^ f ²).

Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Таким образом, чтобы построить плоскость b (n Ç m), перпендикулярную заданной плоскости a (h Ç f), необходимо сначала построить прямую, перпендикулярную данной плоскости (построение прямой а к плоскости ABC дано на рисунке 3.23) и через эту прямую провести искомую плоскость (рисунок 3.24).

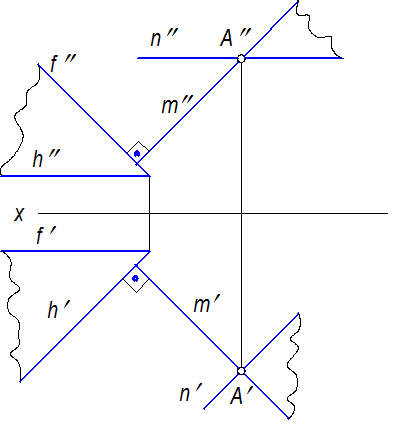
Рисунок 3.24