Уравнения первой степени в пространстве. Всякую плоскость в пространстве геометрически однозначно задать:

Всякую плоскость в пространстве геометрически однозначно задать:

-точкой Мо(х_о;у_о,z_о;) на плоскости и вектором (А;В;С) нормальным к ней;

-точкой Мо(х_о;у_о,z_о;) и расстоянием d от начала координат до плоскости;

-тремя точками на плоскости;

-двумя точками на плоскости и вектором, параллельным ей и т.д.

Во всех случаях – это задачи 2-го типа и решаются они по одной схеме. Пусть плоскость задана точкой Мо(х_о;у_о,z_о;) и вектором (А;В;С) нормальным к ней. Тогда возьмем на плоскости точку М(х;у;z). И тогда векторы М Мо и будут ортогональны и получим А(х- х_о)+В(у- у_о)+С(z- z_о)=0 – уравнение плоскости, проходящей через заданную точку перпендикулярно вектору. Если раскрыть скобки и привести подобные, то получим общее уравнение плоскости Ах+Ву+Сz+D=0. Из этого уравнения видно, что всякое уравнение первой степени с тремя переменными – уравнение плоскости в пространстве. Можно рассматривать частные его случаи в зависимости от значений коэффициентов А,В,С,D.

Типовые задачи на плоскость в пространстве.

1.Разные виды уравнений и переходы от одного к другому виду.

2.Расстояние от точки до плоскости.

3.Угол между плоскостями (и взаимное расположение плоскостей).

4.Точка пересечения плоскостей.

5.Пучок плоскостей и др. более сложные задачи.

Комментарий. Следует запомнить жестко наиболее простую для аналитической геометрии ситуацию: для поиска уравнения плоскости следует указать точку, через которую полоскость проходит, и вектор, нормальный плоскости.

Прямую линию в пространстве в аналитической геометрии задают в виде

пересечения двух плоскостей или .

Можно того же результата добиться, задав прямую проходящей через две заданные точки Мо(х_о;у_о,z_о) и М₁(х₁;у₁;z₁). Тогда из условий параллельности(коллинеарности) векторов ММо и МоМ₁ получим . Если же обозначить вектор МоМ₁ = (m;n;p), то получим канонические уравнения прямой в пространстве . В последних двух способах задания прямой в пространстве “потеряны” уравнения двух плоскостей. Комментарием к этому может служить такое указание – мы имеем равенство трех отношений. Так что, фактически, мы имеет даже три плоскости вместо двух (если сравнивать по два разных отношения, то всегда получится уравнение первого порядка в пространстве – уравнение плоскости). Особенностями этих плоскостей будет следующее – каждая из них является проектирующей данную прямую на некоторую координатную плоскость (в каждом уравнении плоскости только две переменные – значит плоскость перпендикулярна координатной плоскости).

Важно уметь делать переход от одного вида уравнения к другому и понимать смысл этих математических действий в геометрии.

Пример 6.2. Найти, если таковая имеется, точку пересечения трех плоскостей 2х+2у+z=19,

x+2y+4z=31, Решение.Сразу видно, что ранг основной и расширен-

4x+6y+9z=-2. ной матриц не болше 3 и не меньше 2. Для уточнения вычислим = =0. Т.о. rancA=2. Для расширенной матрицы имеем 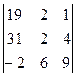= 0. Т.е. rancA’=3. Система противоречива – точки пересечения нет. Геометрически это говорит в данном случае о такой ситуации: параллельных плоскостей нет; следовательно плоскости попарно пересекаются и образуют подобие треугольной призмы.

При взаимном расположении прямой и плоскости следует учитывать, что: полскость характеризуется норамлью и точкой Мо(х_о;у_о,z_о) на плоскости, а прямая – направляющим вектором (m;n;p) и точкой М₁(х₁;у₁;z₁) на прямой.

Так, если плоскость параллельна прямой, то имеем всегда =0, а если плоскость перпендикулярна прямой,то всегда коллинеарен . Если требуется найти точку пересечения прямой и плоскости, то систему

Ах+Ву+Сz+D=0

можно (и даже лучше) решать так: последнее отношение приравнять параметру t; затем выразить через параметр переменные x,y,z (x=mt+ х_о, e=nt+y_о, z=pt+z_о; затем найденное подставить в уравнение плоскости и найти значение параметра t для точки пересечения; после этого вычислить координаты точки пересечения через значение параметра.