 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Сумма конечного числа б. м. (б. б.) слагаемых разного порядка малости (роста) эквивалентна слагаемому самого низкого (высокого) порядка малости (роста)
|
|
4. Если б. м. ф. α (x) ~ α 1(x) при x → a, A =const ≠ 0, то A + α (x) ~ A + α 1(x) при x → a.
Например.  .
.
Чтобы вычислить предел  ,
,
можно воспользоваться основным логарифмическим тождеством  .
.
Например. 
 .
.
Если же  ,
,
то есть в случае неопределенность вида  ,
,
можно применить следующую последовательность тождественных преобразований:
 .
.
Например.
 .
.
3.2. Непрерывность функции одного аргумента
| Определение непрерывной на интервале (а, b) функции | Функция называется непрерывной на интервале (a, b), если она непрерывна в каждой точке этого интервала. |
Определение предела справа для функции f (x):

| Число A называется пределом справа для функции f(x) при х, стремящемся к a ( ), если для любого сколь угодно малого положительного числа ), если для любого сколь угодно малого положительного числа   существует такое положительное число существует такое положительное число  , зависящее от , зависящее от 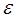  , что для всех значений х из области определения функции, удовлетворяющих неравенству , что для всех значений х из области определения функции, удовлетворяющих неравенству  , следует выполнение неравенства , следует выполнение неравенства  . .
|
Точки х берутся справа от точки х = а.
Правосторонний предел обозначают также  .
.
Определение предела слева для функции f (x):

| Число A называется пределом слева функции f(x) при х,
стремящемся к a ( ), если для любого сколь угодно малого положительного числа ), если для любого сколь угодно малого положительного числа 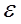  существует такое положительное число существует такое положительное число 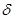 , зависящее от , зависящее от   , что для всех значений х из области определения функции, удовлетворяющих неравенству: , что для всех значений х из области определения функции, удовлетворяющих неравенству:  , следует выполнение неравенства: , следует выполнение неравенства: 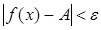 . .
|
Точки х берутся слева от точки х = а.
Левосторонний предел обозначают также  .
.
| Теорема о необходимых и достаточных условиях существования предела А функции f (x) в точке х = а |
Предел А функции f (x ) в точке х = а существует тогда и только тогда, когда существуют односторонние пределы этой функции в точке х = а и эти односторонние пределы равны между собой:
 , или , или 
|
Определение непрерывной на отрезке  функции функции
| Функция f (x) называется непрерывной на отрезке  , если она непрерывна на интервале (a, b) и в точке
х = а – справа ( , если она непрерывна на интервале (a, b) и в точке
х = а – справа ( ), а в точке
х = b – слева ( ), а в точке
х = b – слева ( ). ).
|
| Определение точек разрыва функции | Точки, в которых нарушается хотя бы одно из трех условий непрерывности функции, называются точками разрыва графика функции, или просто точками разрыва. |
| Определение точек устранимого разрыва функции | Односторонние пределы функции в исследуемой точке конечны и равны между собой. В самой точке функция не определена или не задана. |
| Определение точек разрыва первого рода функции | Односторонние пределы функции в исследуемой точке конечны, но не равны между собой. |
| Определение точек разрыва второго рода функции | Хотя бы один из односторонних пределов функции в исследуемой точке равен бесконечности или не существует. |
Элементарные функции терпят разрыв в точках, не принадлежащих области их определения.
Функция кусочно-аналитическая (состоит из «кусочков» аналитических, то есть элементарных, функций), не является элементарной. Такая функция может иметь разрыв в точках, где эта функция не определена, а также в точках, где происходит переход от одного аналитического задания функции к другому (от одной формулы к другой) – это точки, «подозрительные» на разрыв. В точке, «подозрительной» на разрыв, функция может оказаться непрерывной, если в этой точке выполняются все три условия непрерывности функции:
1. Функция определена в точке;
2. Существует конечный предел функции в этой точке;
3. Предел функции в точке равен значению функции в этой точке.
Для исследования элементарной функции на непрерывность можно применить такой план:
1. Найти точки, которые не принадлежат области определения данной функции.
2. Вычислить односторонние пределы функции в этих точках.
3. Сделать вывод о характере разрыва функции в исследуемых точках.
Для исследования кусочно-аналитической функции на непрерывность можно предложить такой план:
1. Найти точки, в которых данная функция не определена – точки разрыва графика функции.
2. Указать точки, в которых происходит переход от одной формулы задания функции к другой формуле, - точки, «подозрительные» на разрыв.
3. Вычислить односторонние пределы функции во всех этих точках (найденных по предыдущим двум пунктам плана).
4. Сделать вывод о характере разрыва или о непрерывности функции в исследуемых точках.
Дата публикования: 2015-10-09; Прочитано: 284 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
