Лагранждық интерполяциялық көпмүшелігінің көмегімен сандық дифференциалдау

(1) теңдікті пайдалана отырып, (8) Лагранж көпмүшелігін -нің функциясы ретінде бойынша дифференциалдайық, сонда:

жуық теңдік аламыз. (5.3) –тен және болатынын ескерсек

(9) аламыз.

(9) формуланы пайдаланып, сегментінде (бұл кезде параметр 1 ден -ге дейінгі мәндерді қабылдайды) тең түйіндерде берілген 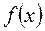функциясының туындысының жуық мәнін есептеуге болады. Сол сияқты функциясының жоғарғы ретті туындыларын табамыз.

Мысал. Төмендегі кестемен берілген функциясының туындысының нүктедегі мәнін табындар.

5.2 кесте

x
f (x)		-1

Шешуі: (9) формуланы пайдаланып (мұнда )

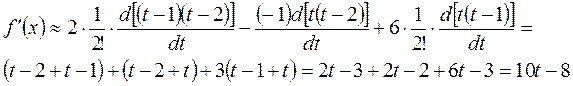
болатынын есептеп табамыз.

Енді түйін мәніне сәйкес келетінін 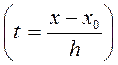ескерсек, болатынын көреміз.

Егер функциясының аналитикалық өрнегі белгілі болса, онда сандық дифференциалдаудың қателігін итерполяциялау қателігінің формуласын (см п. 4.6 с. 88) пайдаланып табамыз, яғни

(10)

мұндағы мән -тен және түйіндерден өзгеше болатын кесіндісіндегі мән. (5.2) ескерсек және функциясы рет дифференциалданады десек, онда

(11)

формуланы аламыз.

Егер туындының мәні кестедегі түйінде табылатын болса. (11) формула әжептәуір қарапайым түрге көшеді. Бұл жағдайда (7)-ні ескеріп

(12)

формула аламыз, мұндағы мән мәндердің арасынан алынған мән.

белгілеу енгізсек, сандық дифференциал-даудың түйіндердегі абсоют қателігін бағалаудың төмендегідей формуласын аламыз:

(13)