Метод дотичних (метод Ньютона)

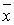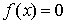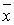Теорема про збіжність методу Ньютона. Нехай - простий корінь рівняння , в деякій околиці якого функція двічі безперервно диференційована. Тоді знайдеться така мала - околиця кореня , що при довільному виборі початкового наближення з цієї околиці ітераційна послідовність методу Ньютона не виходить за межі околиці і справедлива оцінка

, где , .

Нехай маємо функцію на проміжку 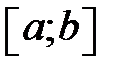, позначивши проведемо дотичну до графіку функції в точці х=х₀, рівняння якої матиме вигляд , звідки легко помітити, що наступне наближення ; після цього проведемо дотичну до графіку функції в точці х=х₁ і т.д..

Рисунок 4.3 – Геометрична інтерпретація розв’язку рівнянь методом дотичних

Звідки отримаємо , процес закінчується якщо .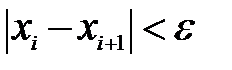

В деяких випадках швидше призводить до результату (вимагає меншого числа послідовних наближень) модифікований метод, що відрізняється відметода хорд тим, що кожна нова хорда проводиться не через точки B₀ і B_n (або A₀ і A_n), а через точку B_n [x_n, f (x_n)] і точку B_n-1 [x_{n-1, f (xn-1})], що відповідають попередньому наближенню (рис. 2.4).

Такий метод, як видно, виявляється близьким до методу дотичних, якщо дотична, проведена в точці B_n, замінюється хордою, що проходить через цю точку і попередню B_n-1.

Рисунок 4.4. – Модифікований метод Ньютона

Відповідні формули методу виходять з формул методу дотичних за умови заміни значення похідної f '(x_n) її наближеним значенням

Умова закінчення обчислень для досягнення заданої точності

| x_n+1 - x_n | ≤ɛ.

Правило вибору початкового наближення зберігається тим же, що і в методі дотичних. А саме, в якості початкової точки вибирається той з кінців інтервалу [a, b ], в якому f (x) f "(x)> 0.

Для проведення хорди тепер необхідно задати ще одне значення x₁, розташоване всередині інтервалу [a, b] так, щоб

f (x₀) f (x₁) > 0.

4. Метод ітерацій (послідовних наближень)

Теорема про збіжність методу простої ітерації. Нехай в деякій - околиці кореня 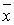функція 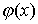диференційована і задовольняє нерівності 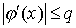, де - постійна. Тоді незалежно від вибору початкового наближення із зазначеної - околиці ітераційна послідовність не виходить з цієї околиці, метод збігається зі швидкістю геометричної послідовності і справедлива оцінка похибки:

, .

Для використання цього методу вихідний нелінійний вираз записується у вигляді .

Нехай відомо початкове наближення кореня . Підставляючи це значення в праву частину рівняння отримуємо нове наближення: .

Далі підставляємо кожний раз нове значення кореня в рівняння отримуємо послідовність значень , n=1, 2, ….

Ітераційний процес припиняється, якщо: .

Рисунок 4.5 – Геометрична інтерпретація розв’язку рівнянь методом послідовних наближень

Ключовий момент у застосуванні методу простої ітерації полягає в еквівалентному перетворенні рівняння. Спосіб, при якому виконується умова збіжності методу простої ітерації, полягає в наступному: вихідне рівняння приводиться до вигляду 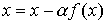. Припустимо додатково, що похідна знакопостоянна і на відрізку [a,b]. Тоді при виборі ітераційного параметра метод збігається і значення

.