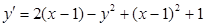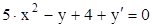Цель работы – ознакомление с методами численного решения обычных дифференциальных уравнений

6.1 Основные сведения

Дифференциальное уравнение (ДУ) − это уравнение, которое содержит неизвестные функции, независимые переменные и производные неизвестных функций.

Решить ДУ − значит найти неизвестные функции.

В зависимости от числа независимых переменных ДУ делятся на две категории:

- обычные дифференциальные уравнения (ОДУ), которые содержат одну независимую переменную;

- уравнение в частных производных, которые содержат несколько независимых сменных.

В данной работе будут рассматриваться только ОДУ.

Общий вид ОДУ:

,

где х − независимая сменная, у − неизвестная функция, - производные неизвестной функции.

Общее решение ОДУ имеет вид:

.

Частное решение ОДУ получается из общего, если произвольным постоянным придать определенные значения. Чтобы получить частное решение, необходимо задать дополнительные условия. ДУ вместе с дополнительными условиями называется заданием. Существует два типа дополнительных условий и, соответственно, два типа заданий:

1) начальные условия (если х − время):

, , …, .

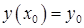Задача решения ОДУ с начальными условиями называется задачей Коши.

2) граничные (краевые) условия (если х − некоторая координата, которая меняется от a до b):

, , …, ;

, , …, .

Задача решения ОДУ с граничными условиями называется краевой задачей.

В данной работе будет рассматриваться задача Коши.

Результатом решения задачи Коши численными методами является таблица значений функции в отдельных точках.

Для решения задачи Коши в работе предлагается применять следующие одношаговые методы: метод Эйлера, метод Эйлера-Коши и метод Рунге-Кутта 4-го порядка.

Метод Эйлера:

, ,

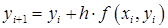где , - шаг расчетов.

Метод Эйлера-Коши:

- вычисляется значение функции в следующей точке по методу Эйлера:

;

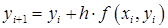- вычисляется приближенное значение производной в конце интервала с использованием :

;

- определяется среднее арифметическое между значениями производной в начале и в конце интервала и находится более точное значение :

.

Метод Рунге-Кутта 4-го порядка:

,

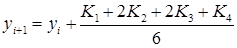где

; ;

; .

6.2 Порядок выполнения работы

1. Решить на ЭВМ дифференциальное уравнение (табл. 6.1) на заданном отрезке изменения аргумента [0; 2] с заданными начальными условиями (y (0) = 1) и шагом расчетов h = 0,25 методами Эйлера, Эйлера-Коши и Рунге-Кутта 4-го порядка.

2. Первые две итерации каждого метода записать подробно (рассчитать «вручную»).

3. Проверить решение дифференциального уравнения с помощью существующих готовых функций (например, встроенных в Mathcad функций rkfixed или rkadapt).

6.3 Содержание отчета

1. Цель работы.

2. Исходные данные для выполнения работы.

3. Результаты решения дифференциального уравнения на ЭВМ разными методами.

4. Подробные расчеты первых двух итераций каждого метода «вручную».

5. Результаты проверки по помощи существующих функций.

Контрольные вопросы

1. Какие существуют категории дифференциальных уравнений в зависимости от числа сменных?

2. Какие типы дополнительных условий (задач) существуют?

3. Что является результатом решения задачи Коши численными методами?

4. Какие одношаговые методы можно использовать для решения задачи Коши?

5. Как выполняется решения ДУ по методу Эйлера?

6. Чем отличается решения ДУ по методу Эйлера и методу Эйлера-Коши?

7. Как выполняется решения ДУ по методу Рунге-Кутта 4-го порядка?

Таблица 6.1 – Исходные дифференциальные уравнения