Экстремум функции двух переменных. Необходимые условия экстремума. Критические и стационарные точки. Достаточные условия экстремума. Схема исследования на экстремум

Рассмотрим функцию z=f(x;y) двух переменных,определенную в некоторой области D.

Точка M0(x0;y0) называется точкой максимума (минимума) функции z=f(x;y), если существует окрестность точки М, такая, что для всех точек (х,у) из этой окрестности выполняется неравенство f(x0,y0)≥f(x;y)(f(x0;yo)≤f(x;y).

Максимумы и минимумы функции называются локальными экстремумами M0(x0;y0)-точкой экстремума.

Теорема1 (необходимые условия экстремума). Если z=f(x;y) дифференцируемая функция и достигает в точке M0(x0;y0) экстремума, то ее частные производные первого порядка в этой точке равны нулю: z’x(M0)=0; z’y(M0)=0.

Точки в которых частные производные первого порядка обращаются в 0(или не существуют), называются критическими или стационарными. Исследование их на экстремум проводят с помощью достаточных условий существования экстремума функции двух переменных.

Пусть M0(x0;y0)-стационарная точка функции z=f(x;y).

Составим выражение ∆=z’’xxˑz’’yy-(z’’xy) .

Теорема 2(достаточные условия экстремума)

1. Если ∆ 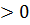и z’’xx 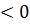, то M0(x0;y0)- точка максимума.

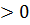2. Если ∆ и z’’xx , то M0(x0;y0)- точка минимума.

3. Если ∆ 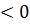, то M0(x0;y0) не является точкой экстремума

4. Если ∆=0, то точка M0(x0;y0) может, как быть, так и не быть точкой экстремума, поэтому требуется дополнительное исследование.

Схема исследования на экстремум.

1. Найти частные производные z’x и z’y

2. Решить систему уравнений z’x=0 и z’y=0 и найти критические точки

3. Найти частные производные z’’xx, z‘’yy, z’’xy, вычислить их значение в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов.

4. Найти экстремумы (экстремальные значения) функции.