 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Асимптоты графика функции. Горизонтальные, вертикальные и наклонные асимптоты. Способы нахождения асимптот
|
|
Асимптота – это прямая, к которой бесконечно близко приближается график функции, при этом он должен бесконечно далеко удаляться от начала координат.
На плоскости асимптоты классифицируют по их естественному расположению:
1) Вертикальные асимптоты, которые задаются уравнением вида  , где «альфа» – действительное число. Популярная представительница
, где «альфа» – действительное число. Популярная представительница 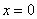 определяет саму ось ординат, вспомним,н-р, гиперболу
определяет саму ось ординат, вспомним,н-р, гиперболу  . Вертикальная асимптота графика, как правило, находится в точке бесконечного разрыва функции. Всё просто: если в точке
. Вертикальная асимптота графика, как правило, находится в точке бесконечного разрыва функции. Всё просто: если в точке  функция
функция 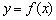 терпит бесконечный разрыв, то прямая, заданная уравнением
терпит бесконечный разрыв, то прямая, заданная уравнением  является вертикальной асимптотой графика. Таким образом, чтобы установить наличие вертикальной асимптоты
является вертикальной асимптотой графика. Таким образом, чтобы установить наличие вертикальной асимптоты  в точке
в точке  достаточно показать, что хотя бы один из односторонних пределов
достаточно показать, что хотя бы один из односторонних пределов 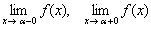 бесконечен. Чаще всего это точка, где знаменатель функции равен нулю. По существу, мы уже находили вертикальные асимптоты в последних примерах урока о непрерывности функции. Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова – любите и жалуйте вертикальную асимптоту. Простейшая иллюстрация:
бесконечен. Чаще всего это точка, где знаменатель функции равен нулю. По существу, мы уже находили вертикальные асимптоты в последних примерах урока о непрерывности функции. Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова – любите и жалуйте вертикальную асимптоту. Простейшая иллюстрация:  и ось ординат (см. Графики и свойства элементарных функций).
и ось ординат (см. Графики и свойства элементарных функций).
Из вышесказанного также следует очевидный факт: если функция непрерывна на  , то вертикальные асимптоты отсутствуют.
, то вертикальные асимптоты отсутствуют.
Наклонные асимптоты традиционно записываются уравнением прямой с угловым коэффициентом. Иногда отдельной группой выделяют частный случай –горизонтальные асимптоты. Например, та же гипербола с асимптотой. Наклонные асимптоты графика функции
Наклонные (как частный случай – горизонтальные) асимптоты могут нарисоваться, если функция стремится к «плюс бесконечности» или/и «минус бесконечности». Поэтому график функции не может иметь больше 2-х наклонных асимптот. Например, график экспоненциальной функции  обладает единственной горизонтальной асимптотой при
обладает единственной горизонтальной асимптотой при  , а график арктангенса
, а график арктангенса  при
при  – двумя такими асимптотами, причём различными.
– двумя такими асимптотами, причём различными.
Когда график и там и там сближается с единственной наклонной асимптотой, то «бесконечности» принято объединять под единой записью  . Например, …правильно догадались:
. Например, …правильно догадались:  .
.
Общее практическое правило:
Если существуют два конечных предела 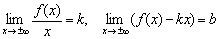 , то прямая
, то прямая  является наклонной асимптотой графика функции
является наклонной асимптотой графика функции 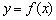 при
при  . Если хотя бы один из перечисленных пределов бесконечен, то наклонная асимптота отсутствует.
. Если хотя бы один из перечисленных пределов бесконечен, то наклонная асимптота отсутствует.
Нахождение асимптот графика функции основано на следующих утверждениях.
Теорема 1. Пусть функция  определена хотя бы в некоторой полуокрестности точки
определена хотя бы в некоторой полуокрестности точки  и хотя бы один из ее односторонних пределов в этой точке бесконечен, т.е. равен
и хотя бы один из ее односторонних пределов в этой точке бесконечен, т.е. равен  или
или  . Тогда прямая
. Тогда прямая  является вертикальной асимптотой графика функции.
является вертикальной асимптотой графика функции.
Таким образом, вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа).
Теорема 2. Пусть функция  определена при значениях аргумента, достаточно больших по абсолютной величине, и существует конечный предел функции
определена при значениях аргумента, достаточно больших по абсолютной величине, и существует конечный предел функции  . Тогда прямая
. Тогда прямая  есть горизонтальная асимптота графика функции.
есть горизонтальная асимптота графика функции. 
Может случиться, что 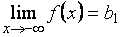 , а
, а  , причем
, причем  и
и  - конечные числа, тогда график имеет две различные горизонтальные асимптоты: левостороннюю и правостороннюю. Если же существует лишь один из конечных пределов
- конечные числа, тогда график имеет две различные горизонтальные асимптоты: левостороннюю и правостороннюю. Если же существует лишь один из конечных пределов  или
или  , то график имеет либо одну левостороннюю, либо одну правостороннюю горизонтальную асимптоту.
, то график имеет либо одну левостороннюю, либо одну правостороннюю горизонтальную асимптоту.
Теорема 3. Пусть функция  определена при значениях аргумента, достаточно больших по абсолютной величине, и существуют конечные пределы
определена при значениях аргумента, достаточно больших по абсолютной величине, и существуют конечные пределы  и
и  . Тогда прямая
. Тогда прямая  является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  .
.
Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет.
Наклонная асимптота так же, как и горизонтальная, может быть односторонней.
Преобразование графиков. Сдвиг по горизонтали и вертикали. Растяжение по горизонтали и вертикали. Отражение относительно вертикальной и горизонтальной оси (все случаи с примером на графике).
График функции y=f(x)+B получается параллельным переносом графика функции y=f(x) в положительном направлении вдоль оси Оу на расстояние В, если В>0 и в отрицательном направлении вдоль оси Оу, если B<0.


График функции y=f(x+b) получается параллельным переносом графика функции y=f(x) в положительном направлении вдоль оси Оx на расстояние b, если b<0 и в отрицательном направлении вдоль оси Оx, если b>0.


Отображение
График функции y=-f(x) получается симметричным отображением графика y=f(x) относительно оси Ох.


График функции y=f(-x) получается симметричным отображением графика y=f(x) относительно оси Оу.
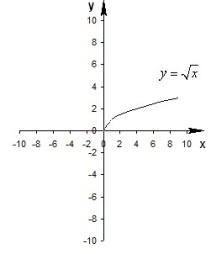

Деформация (растяжение и сжатие) графика
График функции y=Af(x), получается растяжением графика y=f(x) вдоль оси Оу от оси Ох в A раз при A>1 или сжатием вдоль оси Оу к оси Ох в 1/А раз при A<1.


Отражение
График функции 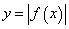 получается из графика функции y=f(x) следующим образом: часть графика функции y=f(x), лежащая над осью Ох и на оси, остается без изменений, а часть графика, лежащая под осью Ох, отражается симметрично относительно оси Ох на верхнюю полуплоскость.
получается из графика функции y=f(x) следующим образом: часть графика функции y=f(x), лежащая над осью Ох и на оси, остается без изменений, а часть графика, лежащая под осью Ох, отражается симметрично относительно оси Ох на верхнюю полуплоскость.


График функции  получается из графика функции y=f(x) следующим образом: часть графика функции y=f(x), соответствующая неотрицательным значениям аргумента
получается из графика функции y=f(x) следующим образом: часть графика функции y=f(x), соответствующая неотрицательным значениям аргумента  , остается без изменений, а отрицательным значениям аргумента будет соответствовать график, полученный путем симметричного относительно оси Оy отображения части графика, оставленной без изменений.
, остается без изменений, а отрицательным значениям аргумента будет соответствовать график, полученный путем симметричного относительно оси Оy отображения части графика, оставленной без изменений.


Дата публикования: 2015-10-09; Прочитано: 2231 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
