Производная обратной функции

Дифференцируемая монотонная функция f: ] a, b [ → R с необращающейся в нуль производной имеет обратную дифференцируемую функцию f ^-1, производная которой вычисляется по формуле

15. Таблица основных производных.

Производная и дифференциал функции. Геометрический смысл дифференциала. Применение дифференциала для приближенных вычислений. Производные высших порядков. Понятие дифференциала высшего порядка.

Дифференциалом функции y=f(x) называется главная линейная относительно Δх часть приращения ф-ции, равная произведению производной функции на приращение аргумента и обозначаетс dy или df(x): dy=f’(x)*Δx.

Геометрический смысл - это тангенс угла наклона касательной в данной точке к оси ОХ.

Пусть нам известно значение функции y0=f(x0) и ее производной y0' = f '(x0) в точке x0. Покажем, как найти значение функции в некоторой близкой точке x. Как мы уже выяснили приращение функции Δyможно представить в виде суммы Δy=dy+α·Δx, т.е.приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dyили Δy»f'(x0)·Δx.
Т.к., по определению, Δy = f(x) – f(x0), то f(x) – f(x0)≈f'(x0)·Δx.
Откуда
f(x) ≈ f(x0) + f'(x0)·Δx

ППроизводные высших порядков

Дифференцируя функцию y = f(x), получим производную первого порядка

y'= f’ (x). Производная y’= f’ (x) функции y = f(x) есть также функция от x.

Дифференцируя производную первого порядка получим производную второго

порядка (y’)’= y’’= f’’ (x) и т.д. Производная п-го порядка является производной

от производной (п – 1) порядка, т.е. уⁿ=y^n-1

. В данной формуле производная

нулевого порядка это сама функция.

Производные порядка выше первого называются производными высших

порядков.

Начиная с производной четвёртого порядка, производные обозначают римскими

цифрами или числами в скобках (y^V или y⁵- производная пятого порядка)

Пусть функция y = f(x) задана неявно в виде уравнения F(x, y) 0.

Продифференцировав это уравнение по x и разрешив полученное уравнение

относительно y’, найдём производную первого порядка. Продифференцировав по x

первую производную, получим вторую производную от неявной функции. Вторая

производная зависит от x, y и y’. Подставляя уже найденное значение y’ в

выражение второй производной, выразим y’’ через x и y.

Аналогично поступаем для нахождения производной третьего и более высокого

порядков.роизводные высших порядков

17. Основные теоремы дифференциального исчисления (Ферма, Роля, Лагранжа, Коши). Правила Лопиталя.

Теорема Ферма:

Пусть функция определена на и достигает своего наибольшего и наименьшего значения (M и m) в некоторой из . Если существует производная в , то она обязательно равна 0.

Доказательство:

Существует 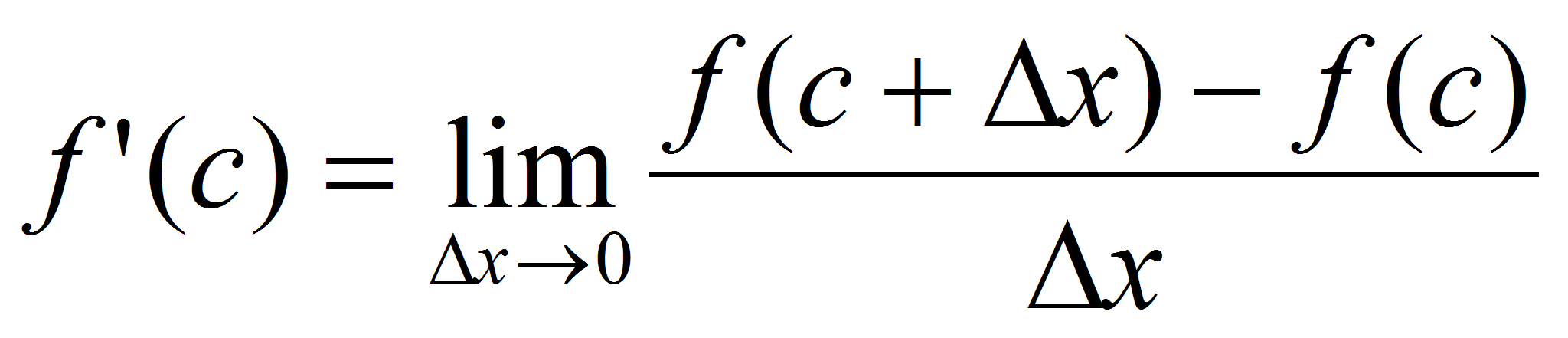. Возможны два случая:

1) , => , => .

2) , => , => .

Из 1) и 2) следует, что

Теорема Ролля (о корнях производной):

Пусть функция непрерывна на и дифференцируема на и на концах отрезка принимает одинаковые значения: . Тогда существует хотя бы одна точка из , производная в которой .

Доказательство:

Непрерывная достигает на M и m. Тогда возможны два случая:

1) , =>

2) наибольшее значение достигается внутри интервала по теореме Ферма.

Теорема Лангража (о конечных приращениях):

Пусть функция непрерывна на и дифференцируема на . Тогда существует хотя бы одна из , для которой выполняется следующее равенство: .

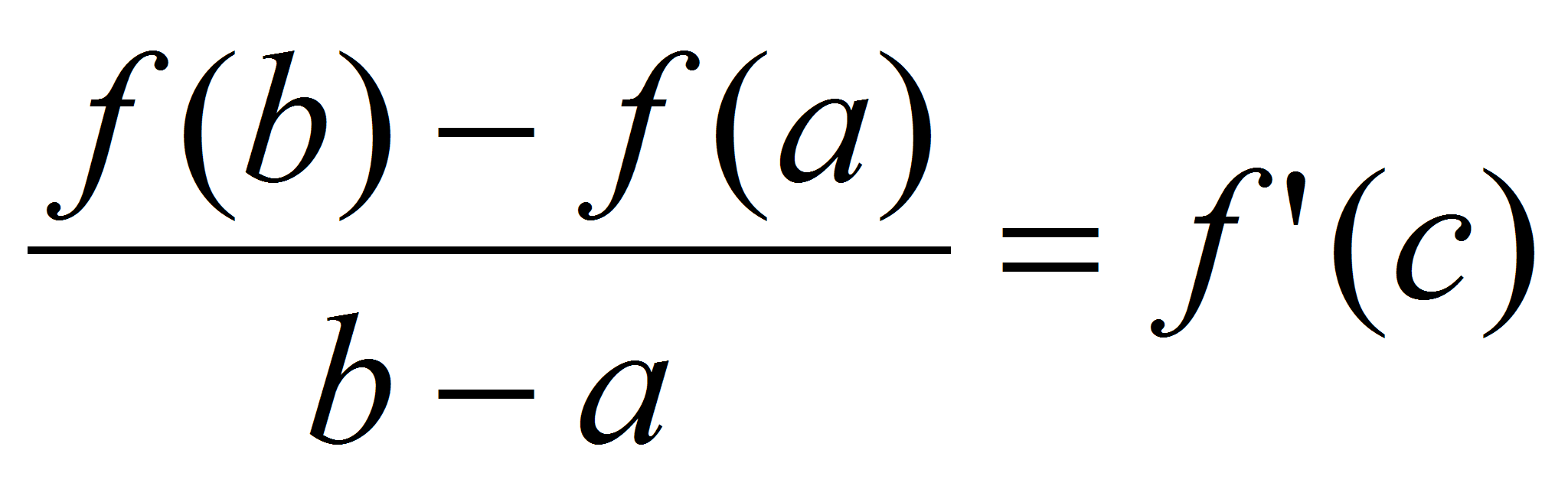Доказательство:

Введем функцию . (непрерывная на и дифференцируемая на ).

,

Функция удовлетворяет Теореме Ролля существует 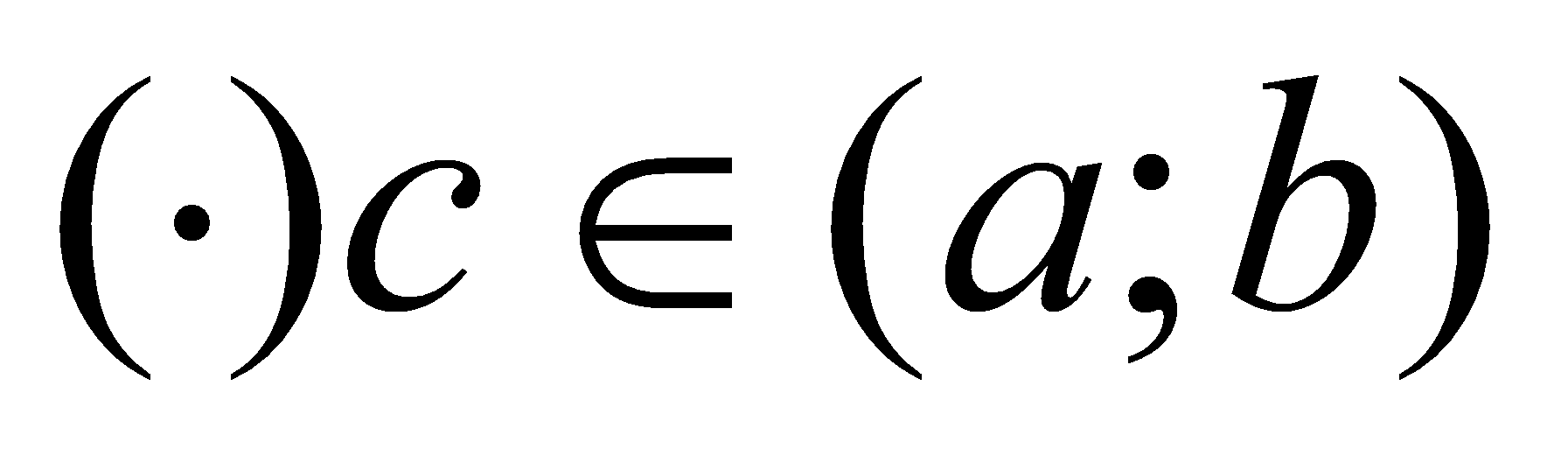, для которой: , , , .

Теорема Коши:

Пусть функции и непрерывны на и дифференцируемы 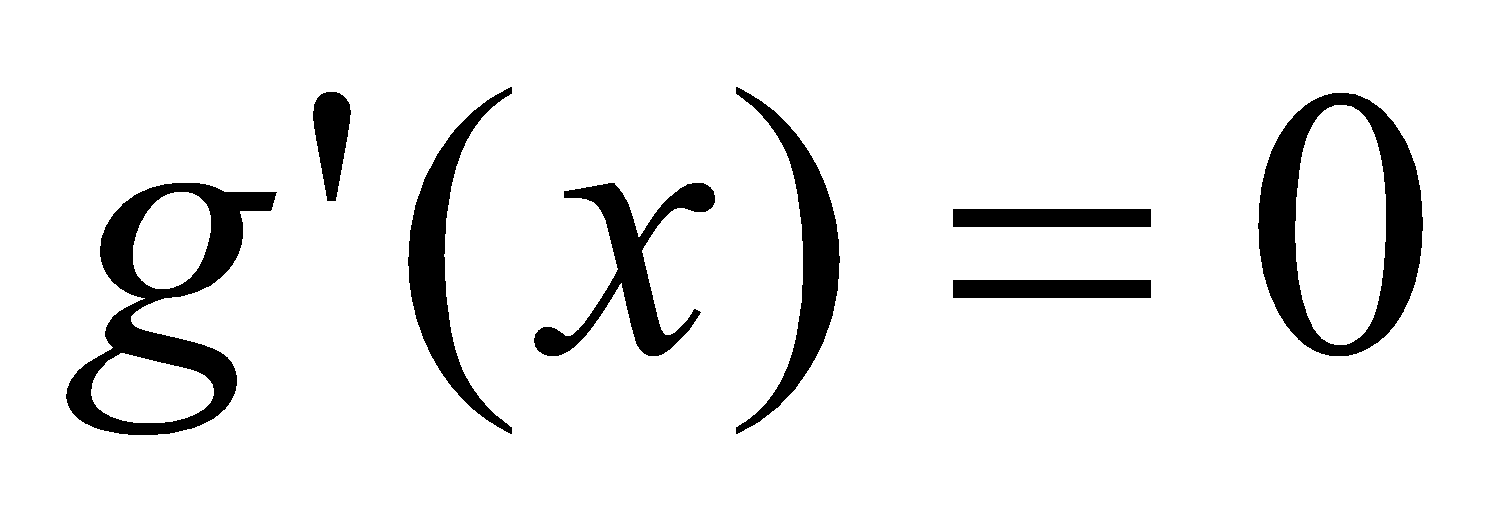на , на . Тогда существует хотя бы одна внутренняя точка , для которой выполняется равенство .

Доказательство:

Введем функцию . (непрерывная на и дифференцируемая на ).

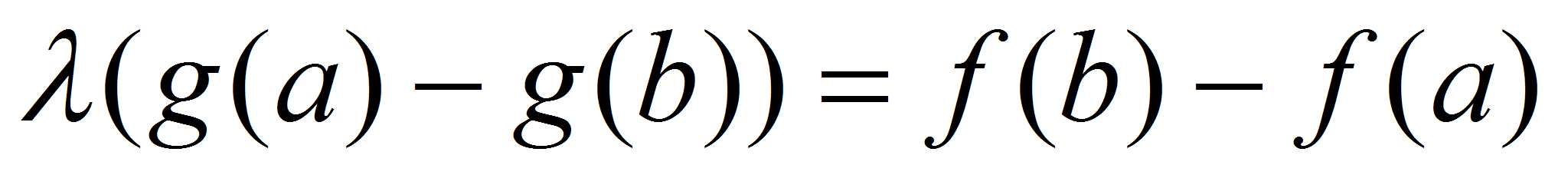
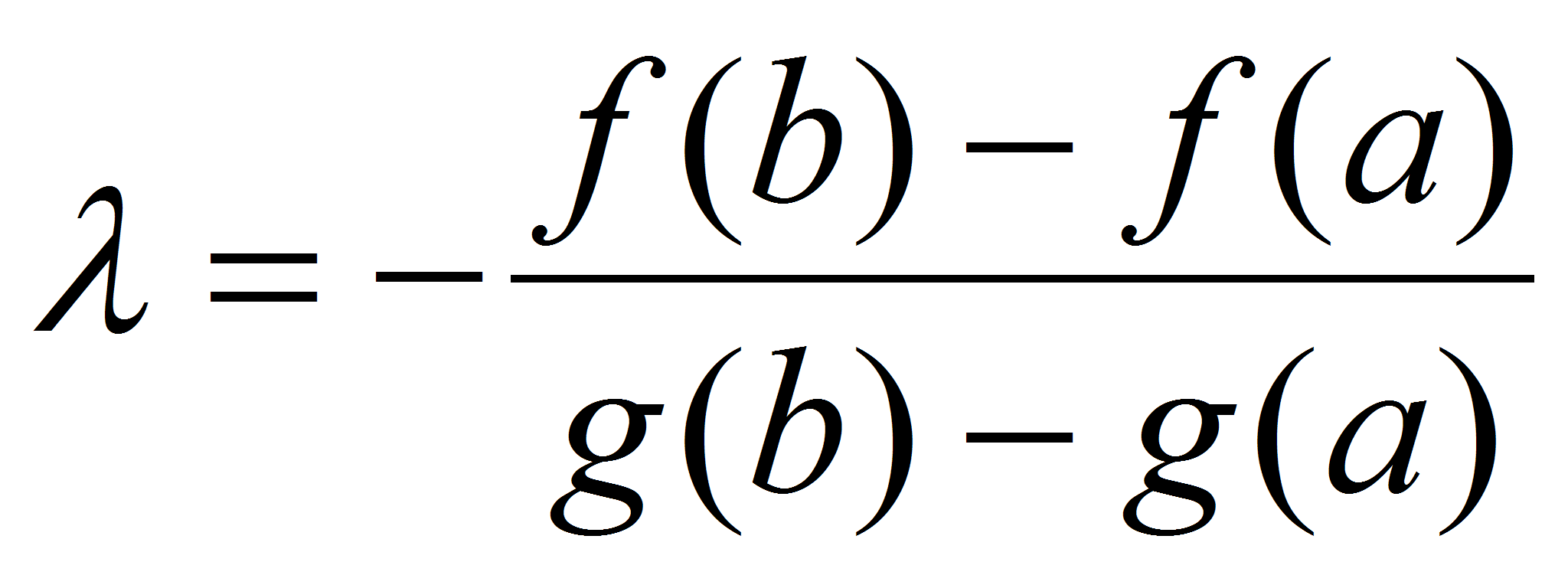
Функция удовлетворяет Теореме Ролля существует 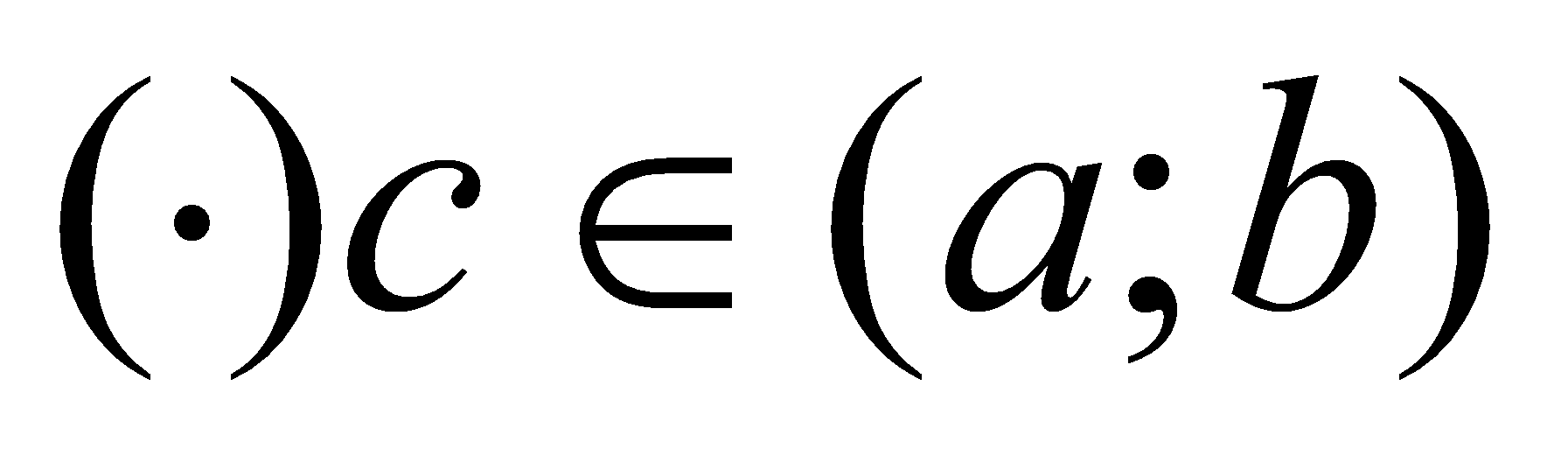, для которой: , , , .

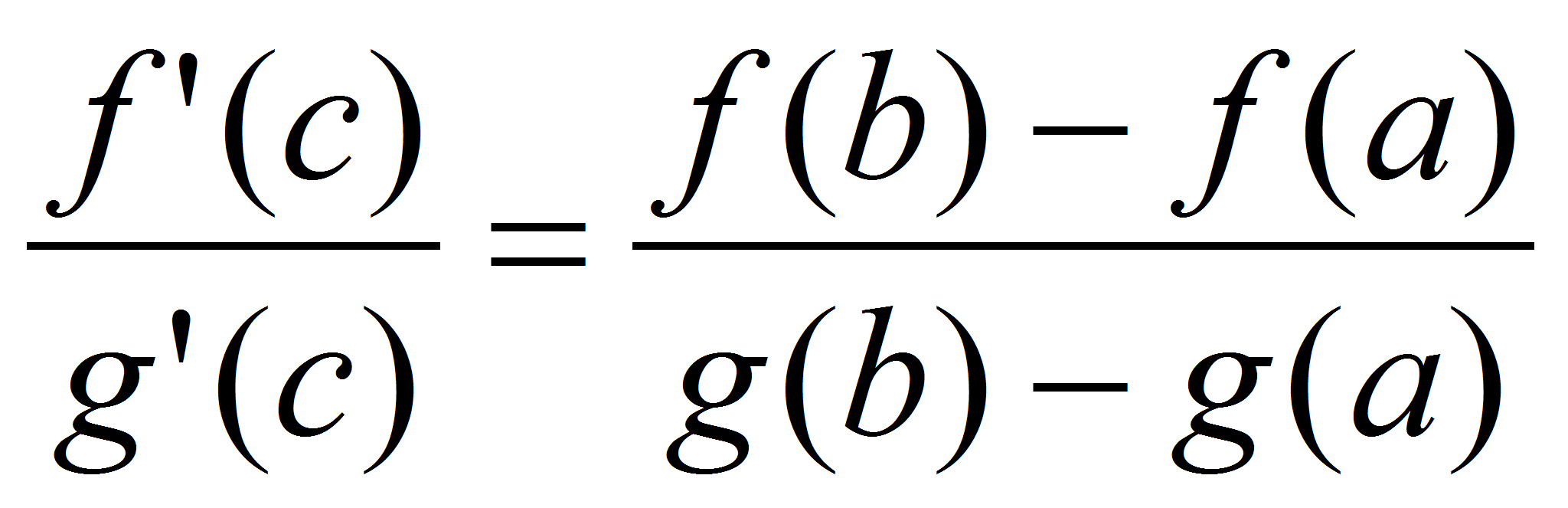Теорема Лопиталя:

Пусть функции и дифференцируемые в некоторой окрестности точки , , 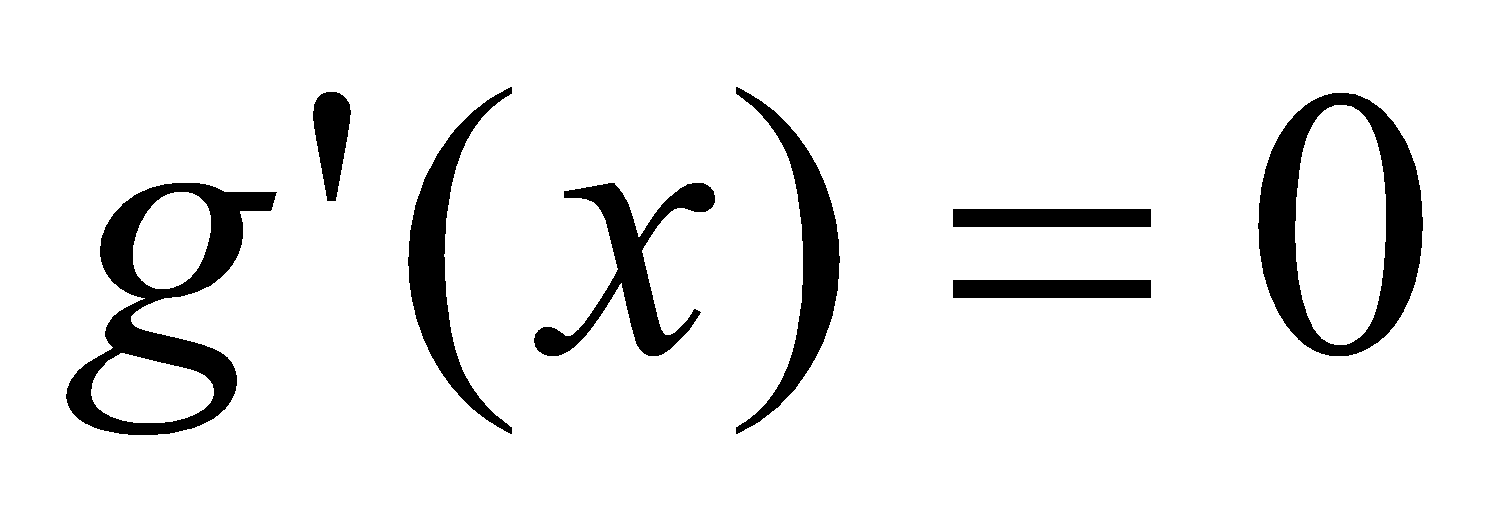функции и либо бесконечно большие, либо бесконечно малые при и существует предел . Тогда существует предел .