Система будет устойчива, если переходные процессы xп(t), вызванные возмущениями, будут зату­хающими, то есть если с течением времени xп(t) будет стремиться к нулю

Решение x_п(t) однородного дифференциального уравнения имеет вид:

(3)

Здесь С_i - постоянные интегрирования, определяющиеся началь­ными условиями и возмущением, l_i - корни характеристического уравнения

D(l) = 0, (4)

где полином D(l), называемый характеристическим, есть левая часть уравнения (1) динамики системы после замены оператора дифференцирования p на комплексную переменную l.

Полином D(l) является знаменателем передаточной функции W_з(p) системы после освобождения в нем от дроби и замены р на l, т. е.

D(l)=R(l)+Q(l), (5)

где R(l) и Q(l) - числитель и знаменатель передаточной функ­ции W(р) разомкнутой системы при замене р на l.

Таким образом, переходный процесс x_п(t) представляет собой сумму составляющих, число которых определяется числом кор­ней l характеристического уравнения (4), то есть порядком урав­нения системы.

В общем случае корни l являются комплексными. При этом они образуют пары сопряженных корней:

,

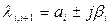где a, может быть положительной или отрицательной величиной. Каждая такая пара корней дает в выражении (3) составляющую переходного процесса, равную

где C¢_i и j _i определяются через С_i, иC_{i +1}.

Эта составляющая представляет собой синусоиду с амплитудой, изменяющейся во времени по экспоненте. При этом, если a_i < 0, эта составляющая будет затухать. Наоборот, при a_I > 0 получатся расходящиеся колебания. Если a_I = 0, что соответствует паре мнимых корней, будут незатухающие синусоидальные колебания.

Условием затухания данной составляющей переходного про­цесса является отрицательность дейст­вительной части a_i соответствующей пары сопряженных корней характери­стического уравнения.

В частном случае, когда b_I = 0, име­ем действительный корень l_I = a_i. Со­ответствующая ему составляющая переходного процесса C_i e^lit пред­ставляет собой экспоненту, которая будет затухать или увеличи­ваться в зависимости от знака a_i.

Таким образом, в общем случае переходный процесс в системе состоит из колебательных и апериодических составляющих. Каждая коле­бательная составляющая обязана своим появлением паре комп­лексных сопряжении корней, а каждая апериодическая - дейст­вительному корню. Отсюда следует, что общим условием затухания всех составляющих, а значит, и всего переходного процесса в целом является отрицательность действительных частей всех корней характеристического уравнения системы, то есть всех полюсов (корней знаменателя) передаточной функции системы.

Если хотя бы один корень имеет положительную действитель­ную часть, он даст расходящуюся составляющую переходного процесса и система будет неустойчивой. Наличие пары сопряжен­ных чисто мнимых корней l_i,i+1=±jb_i даст незатухающую гармоническую составляющую переходного процесса. При этом в системе установятся незатухающие колебания с частотой, равной b_i. Этот случай является граничным между устойчивостью и неустойчивостью - система при этом находится на границе устойчивости. Такая система, очевидно, также неработо­способна, как и неустойчивая.

Если изобразить корни характеристического уравнения системы точками на комплексной плоскости (рис. 2), то найденное выше общее условие устойчивости линейной системы можно сформули­ровать еще так: условием устойчивости системы является располо­жение всех корней характеристического уравнения, т. е. полюсов передаточной функции системы, в левой комплексной полуплоскости или, все они должны быть левыми.

Наличие корня на мнимой оси означает, что система находится на границе устойчивости.

Рисунок 2. – Расположение корней характеристического уравнения САУ