Поляризация электромагнитных волн

Как будет показано в дальнейшем (см. раздел «Излучение электромагнит­ных волн») источники излучения электромагнитных волн, локализованные в ограниченной области, излучают сферическую электромагнитную волну, фронт которой с ростом расстояния от излучателя стремится к плоскости. Отсюда следует, что плоскую волну, рассмотренную в предыдущих разделах, мог возбудить, например, электрический вибратор, ось которого ориентирована вдоль оси “ “ декартовой системы координат. Для этой волны ориентация векторов электромагнитной волны неизменна в пространстве. Такие волны называются линейно - (реже плоско) поляризованными.

Плоскостью поляризации называется плоскость, параллельная направле­нию распространения волны, т.е. по направлению вектора , и вектору напря­женности электрического поля. Для линейнополяризованной волны плоскость поляризации не меняет (во времени) ориентации в пространстве.

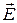Пусть волна создается двумя взаимно перпендикулярными вибраторами, которые ориентированы вдоль осей “ “ и “ “. В этом случае вектор монохроматической электромагнитной волны, создаваемой этими вибраторами на больших расстояниях, может быть представлен в следующем виде:

. (2.24)

Как будет показано ниже, выражение (2.24) в зависимости от соотношения амплитуд Е_xm и Е_ym и разности фаз суммируемых волн описывает волну той или иной поляризации: линейной, круговой и эллиптической.

Поляризация волны – характеристика, которая определяет ориентацию вектора 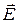. Если плоскость поляризации со временем вращается по часовой стрелке вокруг вектора , то волну называют правополяризованной, если против часовой стрелки – то левополяризованной. Конец вектора 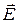при вращении вокруг вектора в общем случае описывает эллипс. Волны такого типа называют эллиптически поляризованными. Волну, у которой малая ось поляризационного эллипса равна большой оси, называют волной круговой поляризации (с левым или правым вращением), а волну, у которой малая ось поляризационного эллипса равна нулю – волной линейной поляризации.

Запишем выражения для модуля вектора 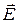волны (2.24) и угла q между осью и вектором 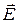. Эти выражения имеют вид:

, (2.25)

Рассмотрим несколько частных случаев задания величин Е_xm, E_ym и j.

1. j = 0, Е_xm и E_ym – произвольные числа.

В этом случае из выражений (2.25) следует, что

, . (2.26)

Из выражения (2.26) видно, что в этом случае формула (2.24) описывает линейнополяризованную волну, плоскость поляризации которой составляет угол q с осью , величина которого определяется отношением величин E_ym и Е_xm.

2. Е_xm = E_ym, j = p/2.

В этом случае из выражений (2.25) следует, что

, . (2.27)

Из выражения (2.27) видно, что в этом случае формула (2.24) описывает волну круговой поляризации с левым вращением.

3. Е_xm = E_ym, j = - p/2.

В этом случае из выражений (2.25) следует, что формула (2.24) описывает волну круговой поляризации с правым вращением.

4. В общем случае при E_ym ¹ E_xm и любом j конец вектора 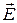описывает в фиксированной точке пространства эллипс. В пространстве по мере распространения волны конец вектора 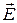движется по цилиндрической поверхности. Рис. 2.2. поясняет положение вектора 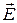левополяризованной волны в фиксированный момент времени.

Приведенный анализ формулы (2.24) показывает, что волну с любым типом поляризации можно представить суммой двух волн, поляризованных линейно в двух ортогональных плоскостях.

Можно показать, что эллиптическую и линейно поляризованную волну можно представить суперпозицией двух волн с круговой поляризацией и противоположными направлениями вращения.