Основы теории теплообмена

Теплообменом называется самопроизвольный необратимый процесс переноса теплоты в пространстве с неоднородным температурным полем в направлении от высокого температурного уровня к низкому.

Существуют три элементарных способа переноса теплоты: теплопроводность, конвекция и тепловое излучение.

Теплопроводностью называется перенос теплоты, обусловленный взаимодействием микрочастиц соприкасающихся тел или частей одного тела с различной температурой. В чистом виде теплопроводность наблюдается в твердых телах, в жидкостях и газах - при условии отсутствия конвекции.

Конвекция - перенос теплоты вследствие пространственного перемещения вещества. Наблюдается в текучих жидкостных и газовых средах и сопровождается теплопроводностью.

Теплопередачей называется процесс переноса теплоты от одной жидкой или газообразной среды к другой через разделяющую их твердую стенку.

Тепловое излучение - перенос теплоты в результате распространения внутренней энергии излучающего тела посредством электромагнитных волн, происходящий с двойным взаимным превращением - теплоты в энергию поля и наоборот.

В реальных случаях переноса теплоты перечисленные элементарные способы обычно сопутствуют друг другу, и если имеют место хотя бы два способа, то теплообмен называют сложным.

Основными количественными характеристиками процесса теплообмена являются температурное поле, температурный напор или разность температур, тепловой поток, плотность теплового потока.

Температурное поле представляет собой совокупность значений температуры всех точек тела в данный момент времени.

Температурный напор - разность между температурами поверхностей твердого тела, среды и стенки или двух сред, между которыми происходит теплообмен.

Тепловым потоком называется количество теплоты, переносимое в единицу времени через рассматриваемую поверхность теплообмена.

Плотность теплового потока - отношение теплового потока к площади теплопередающей поверхности.

Общая кинетическая зависимость для непрерывных процессов теплопередачи, выражающая связь между тепловым потоком Q и поверхностью теплообмена F, представляет собой основное уравнение теплопередачи:

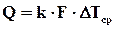,	(1)
где	k	-	коэффициент теплопередачи, определяющий среднюю скорость передачи теплоты вдоль всей поверхности теплообмена;
	F	-	площадь поверхности теплообмена;
	DТ	-	температурный напор или средняя разность температур между теплоносителями, определяющая среднюю движущую силу процесса теплопередачи.

Коэффициент теплопередачи показывает, какое количество теплоты переходит за 1 секунду от более нагретого к более холодному теплоносителю через поверхность теплообмена 1 м² при средней разности температур между теплоносителями, равной 1 градусу.

Основным законом передачи тепла теплопроводностью является закон Фурье, согласно которому количество теплоты dQ, передаваемое посредством теплопроводности через элемент поверхности dF, перпендикулярный направлению теплового потока, за время dt прямо пропорционально температурному градиенту ¶ t / ¶ n, поверхности dF и времени dt:

,	(2)
где	l	-	коэффициент теплопроводности;
	¶ t / ¶ n	-	температурный градиент;
	t	-	время протекания процесса.

Производная температуры по нормали к изотермической поверхности называется температурным градиентом. Градиент является вектором, направление которого соответствует повышению температуры. Величина температурного градиента характеризует наибольшую скорость изменения температуры в данной точке температурного поля. Перемещение теплоты всегда происходит по линии температурного градиента, но направлено в сторону, противоположную этому градиенту, поэтому в формуле (2) стоит знак "-". Знак минус указывает на то, что тепло перемещается в сторону падения температуры.

Плотность теплового потока:

.

(3)

Коэффициент пропорциональности l называется коэффициентом теплопроводности. Коэффициент теплопроводности показывает, какое количество теплоты проходит вследствие теплопроводности в единицу времени через единицу поверхности теплообмена при падении температуры на 1 градус на единицу длины нормали к изотермической поверхности.

Величина l характеризует способность вещества проводить теплоту путем теплопроводности и зависит от природы вещества, его структуры, температуры и некоторых других факторов.

Общим математическим выражением температурного поля в дифференциальной форме является дифференциальное уравнение теплопроводности. В прямоугольных координатах при отсутствии внутренних источников теплоты оно имеет следующий вид:

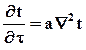,	(4)
где	а	-	коэффициент температуропроводности.
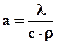.	(5)

Коэффициент температуропроводности характеризует теплоинерционные свойства вещества. При прочих равных условиях быстрее нагреется или охладится то вещество или тело, которое обладает бóльшим коэффициентом температуропроводности.

Для стационарных процессов:

,

(6)

Для решения дифференциального уравнения теплопроводности необходимо знать краевые условия (условия однозначности):

а) геометрические условия, задающие форму и размер тела;

б) физические условия, определяющие физические свойства вещества (l, с, r), их зависимость от температуры, а также изменение во времени мощности внутренних источников теплоты;

в) начальные условия, устанавливающие распределение температуры внутри тела t(x,y,z) в начальный момент времени t = 0. В простейшем случае при t = 0 температура во всех точках тела одинакова: t = tо. Задание начальных условий требуется только для нестационарных процессов;

г) граничные условия, характеризующие процесс теплообмена между поверхностью тела и окружающей его средой.

Различают три рода граничных условий:

· граничные условия первого рода - на поверхности тела задано распределение температуры tп в каждый момент времени, в частности, температура поверхности тела может поддерживаться постоянной;

· граничные условия второго рода - на поверхности тела задано распределение плотности теплового потока qп в каждый момент времени, в частном случае это распределение может быть равномерным и не изменяться во времени;

· граничные условия третьего рода - известны температура среды, окружающей тело, и закон, по которому осуществляется теплообмен между поверхностью тела и средой.

Если среда жидкая, то чаще всего используется закон Ньютона - Рихмана, связывающий плотность теплового потока на поверхности q_п c температурами поверхности t_п и среды t_ж:

,	(7)
где	a	-	коэффициент теплоотдачи, характеризующий эффективность теплообмена.

Коэффициент теплоотдачи показывает, какое количество теплоты передается от 1 м² поверхности стенки к среде (жидкости или газу) или от cреды к 1 м² поверхности стенки в течение 1 секунды при разности температур между стенкой и средой 1 градус.

С понятием теплоотдачи связано понятие конвективного теплообмена.

Конвективным теплообменом или конвективной теплоотдачей называется перенос теплоты между некоторой выделенной поверхностью и движущейся относительно нее текучей средой (жидкостью или газом), который осуществляется совместно теплопроводностью и конвекцией. В качестве выделенной поверхности конвективного теплообмена рассматривается поверхность твердого тела или граница раздела жидкостей или жидкой и газовой фазы.

Вследствие сложной структуры потоков, особенно в условиях турбулентного движения, величина a является сложной функцией многих переменных. Коэффициент теплоотдачи зависит от следующих факторов:

· режима течения среды, т.е. скорости w, коэффициента кинематической вязкости n;

· тепловых свойств жидкой или газообразной среды, определяемых удельной теплоемкостью с_р, теплопроводностью l, а также коэффициентом объемного расширения b;

· геометрических параметров, к которым относятся форма, определяющий размер стенки, шероховатость поверхности стенки.

При рассмотрении стационарных процессов распространения теплоты необходимо знать граничные условия первого рода. В инженерных расчетах часто встречаются задачи определения коэффициента теплопередачи тел простейшей геометрической формы: плоской и цилиндрической стенки.

Коэффициент теплопередачи плоской стенки рассчитывается из уравнения:

,	(8)
где	a1, a2	-	коэффициенты теплоотдачи соответственно внутренней и наружной поверхности стенки;
	d	-	толщина стенки;
	l	-	коэффициент теплопроводности материала стенки.

Коэффициент теплопередачи для цилиндрической стенки при отнесении теплового потока к внутренней поверхности стенки вычисляется из уравнения:

,	(9)
где	r1, r2	-	внутренний и внешний радиусы цилиндрической стенки.

Помимо рассмотренных видов передачи теплоты практически всегда имеет место теплообмен излучением. Все нагретые материальные объекты излучают энергию в окружающее пространство в форме квантов энергии или электромагнитных волн. Длины волн теплового излучения лежат в невидимой инфракрасной части спектра и имеют длину 0,8 - 40 мк.

Коэффициент теплоотдачи при теплообмене излучением рассчитывается на основе закона Hьютона - Рихмана:

,	(10)
где	qл	-	плотность теплового потока;
	Tв	-	температура воздуха;
	Тс	-	температура стенки теплообменного аппарата.

Величина вычисляется на основе уравнения Стефана - Больцмана. Для инженерных расчетов может быть применено упрощенное соотношение:

,	(11)
где	s	-	постоянная Стефана-Больцмана, s = 5,67×10-8 Вт/(м2×К);
	eс	-	коэффициент полного нормального излучения поверхности;
	eв	-	коэффициент полного нормального излучения воздуха.

Hа практике конвективный теплообмен всегда сопровождается лучистым теплообменом, т.е. имеет место сложный теплообмен.

В случае сложного теплообмена общий коэффициент теплоотдачи определяется суммой: