ВВедение. Доказано, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким-либо законам распределения

Нормальный закон распределения (часто называемый зако­ном Гаусса) имеет в статистике широкий круг приложений и за­нимает среди других законов распределения особое положение. Главная особенность, выделяющая нормальный закон среди дру­гих, состоит в том, что он является предельным законом, к кото­рому приближаются другие законы распределения при весьма ча­сто встречающихся условиях.

Доказано, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким-либо законам распределения, приближенно подчиняется нор­мальному закону, и это выполняется тем точнее, чем большее ко­личество случайных величин суммируется. Основное ограниче­ние, налагаемое на суммируемые величины, состоит в том, что они все должны играть в общей сумме относительно малую роль. Если ни одна из случайно действующих величин по своему дейст­вию не окажется преобладающей над другими, то закон распреде­ления очень близко подходит к нормальному.

Такая закономерность проявляется во многих практических случаях. Например, еще Кетле обнаружил, что вариация в одно­родной группе характеризуется нормальной кривой. Если пост­роить эмпирическую кривую распределения людей одной нации, пола и возраста по росту, весу, то она напоминает кривую Гаусса-Лапласа. Поэтому нормальное распределение часто применяется в тех случаях, когда истинный закон распределения известен, но вычисления по этому закону затруднительны, а аппроксимация его нормальным распределением допустима.

Примечание. Несмотря на широкое распространение, нормальное рас­пределение не универсально. Если нет уверенности в его применимости, следует проверить возможность использования нормального распределения для описания случайной величины с помощью критериев согласия.

Уравнение для плотности вероятности нормального распределения име­ет вид

а уравнение интегральной функции нормального распределения

—

Кривая плотности нормального распределения имеет симмет­ричный холмообразный вид (рис.).

Максимальная ордината кривой соответствует точке х = = Mo = Me. По мере удаления от этой точки плотность распределе­ния падает, и при 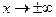кривая асимптотически приближается к оси абсцисс. Изменение средней величины при постоянстве стандартного отклонения σ приводит к сме­щению кривой вдоль оси абсцисс, не меняя ее формы. С увеличе­нием стандартного отклонения кривая становится более пологой, с уменьшением стандартного отклонения — бо­лее острой. Площадь, заключенная под кривой, асимптотически приближающейся к оси абсцисс, равна единице.

Весьма важной практической задачей является определение вероятности того, что случайная величина попадет на заданный интервал вещественной оси (а, b). Она определяется следующей формулой:

Для выполнения работы используйте функцию EXCEL НОРМРАСП и другие связанные с ней функции

ФУНКЦИЯ НОРМРАСП

См. также НОРМОБР, НОРМСТРАСП, НОРМСТОБР, НОРМАЛИЗАЦИЯ.

Синтаксис:

НОРМРАСП (х; среднее; стандартное _ откл; интегральная)

Результат:

Рассчитывает нормальное распределение.

Аргументы:

• х: значение, для которого вычисляется нормальное распре­деление;

• среднее: средняя арифметическая распределения;

• стандартное_откл: стандартное отклонение распреде­ления;

• интегральная: логическое значение, определяющее форму функции. Если аргумент интегральная = 1, то функция НОРМ­РАСП рассчитывает функцию распределения случайной величины(интегральную функцию распределения); если аргумент интегральная = 0 — плотность вероятности случайной величины (дифференциальную функцию рас­пределения).

Замечания:

если аргумент среднее = 0 и аргумент стандартное __откл = =1, то функция НОРМРАСП рассчитывает стандартное нормаль­ное распределение (см. описание функции НОРМСТРАСП).

Функция НОРМРАСП использует первое уравнение, если ар­гумент интегральная = 0, и второе уравнение, если аргумент интегральная = 1.

Так, формула =НОРМРАСП(42;40;1,5;0) рассчитает значение 0,109, а формула =НОРМРАСП(42;40;1,5;1) - значение 0,909.

Пример 1. Для закупки и последующей продажи мужских зимних курток фирмой было проведено выборочное обследова­ние мужского населения города в возрасте от 18 до 65 лет в целях определения его среднего роста. В результате было установлено, что средний рост = 176 см, стандартное отклонение = 6 см. Необходимо определить, какой процент общего числа закупае­мых курток должны составлять куртки 5-го роста (182-186 см). Предполагается, что рост мужского населения города распределен по нормальному закону.

Формула для решения задачи имеет следующий вид:

=НОРМРАСП(186;176;6;ИСТИНА)-НОРМРАСП (182;176;6;ИСТИНА) = 0,95221 - 0,84134 = 0,11086.

Таким образом, куртки 5-го роста должны составлять прибли­зительно 11 % общего числа закупаемых курток.

Функция НОРМОБР

См. также НОРМРАСП, НОРМСТРАСП, НОРМСТОБР, НОРМАЛИЗАЦИЯ, ДОВЕРИТ. Синтаксис:

НОРМОБР (вероятность; среднее; стандартное _ откл) Результат:

Рассчитывает квантиль нормального распределения, т.е. значение признака x_q для которого выполняется условие:

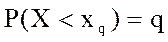
где q – заданная вероятность.

Аргументы:

• вероятность: заданная вероятность q;

• среднее: средняя арифметическая распределения;

• стандартное __ откл: стандартное отклонение распределения.

Замечания:

• если аргумент среднее = 0 и аргумент стандартное _ откл = =1, то функция НОРМОБР использует обратную функцию стандартного нор­мального распределения (см. описание функции НОРМСТОБР);

Математика-статистическая интерпретация:

См. описание функции НОРМРАСП.

Обратная функция нормального распределения используется в ситуациях, когда известна вероятность определенного значения случайной величины и необходимо рассчитать это значение.

Например, формула =НОРМОБР(0,90879;40;1,5) рассчитыва­ет значение 42,00001 (сравните с формулой =НОРМРАСП(42;40; 1,5;1), рассчитывающей значение 0,90879).

На практике часто встречается задача, обратная задаче вычис­ления вероятности попадания нормально распределенной слу­чайной величины на участок, симметричный относительно мате­матического ожидания.

Пример 2. Для задачи, рассмотренной выше, рассчи­тать границы интервала роста мужского населения города, веро­ятность попадания в который случайной величины роста состав­ляет 0,95.Возможны следующие способы решения этой задачи.

1) Необходимо рассчитать квантили уровня 0,025 и 0,975 с помощью функции НОРМОБР. Полученные значения определят соответственно верхнюю и нижнюю границы искомого интервала.

2) Формула для вероятности попадания случайной величины на участок, симметричный относительно математического ожидания, имеет следующий вид:

Следовательно для определения величины ε нужно воспользоваться функцией НОРМОБР:

ε = НОРМОБР((P + 1)/2;0;σ)

Границы искомого интервала –

Функция НОРМСТРАСП

См. также НОРМРАСП, НОРМОБР, НОРМСТОБР, НОРМА­ЛИЗАЦИЯ.

Синтаксис:

НОРМСТРАСП (z)

Результат:

Рассчитывает стандартное нормальное распределение.

Аргументы

: z:. значение, для которого вычисляется стандартное нормаль­ное распределение.

Математика-статистическая интерпретация:

См. описание функции НОРМРАСП.

Стандартное нормальное распределение представляет собой не что иное, как «обычное» нормальное распределение, у которо­го среднее равно нулю, а стандартное отклонение — единице.

Особое выделение функции стандартного нормального рас­пределения связано с тем, что она используется при вычислении функций нормального распределения с другими значениями и σ (отличными от 0 и 1 соответственно). Практически во всех учебниках по тео­рии вероятностей и теории статистики приведены таблицы для функции стандартного нормального распределения. Поэтому, если нет под рукой компьютера, можно производить расчеты вручную, используя таблицы. Для этого необходимо выполнить преобразование

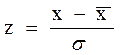
Например, формула =НОРМСТРАСП((42-40)/1,5) рассчита­ет значение 0,90879, такое же как и формула =НОРМРАСП(42;40; 1,5;1) (см. описание функции НОРМРАСП).

Функция НОРМСТОБР

См. также НОРМРАСП, НОРМОБР, НОРМСТРАСП, НОР­МАЛИЗАЦИЯ.

Синтаксис:

НОРМСТОБР (вероятность)

Результат:

Рассчитывает квантиль стандартного нормального распределе­ния.

Аргументы:

вероятность: вероятность, соответствующая нормальному распределению.

Математика-статистическая интерпретация:

См. описание функций НОРМСТРАСП, НОРМОБР.

Обратная функция стандартного нормального распределения рассчитывает квантиль z_q.

Например, формула =НОРМСТОБР(0,69146) вычисляет зна­чение 0,5 (сравните с формулой =НОРМСТРАСП(0,5), рассчиты­вающей значение 0,69146). Кроме того, формула =НОРМСТОБР (0,69146) может быть заменена формулой =НОРМОБР(0,69146; 0;1), также рассчитывающей значение 0,5 (см. описание функции НОРМОБР).

Функция ДОВЕРИТ

См. также НОРМАЛИЗАЦИЯ, НОРМОБР, НОРМРАСП, НОРМСТОБР, НОРМСТРАСП, ZTECT.

Синтаксис: •

ДОВЕРИТ (альфа; станд _ откл; размер) Результат: Рассчитывает значение предельной ошибки выборки.

Аргументы:

• альфа: уровень значимости, используемый для вычисления уровня надежности. Уровень надежности равняется 100 (1—альфа) % (например, альфа, равное 0,05, означает 95%-ный уровень надеж­ности).

• станд _ откл:. стандартное отклонение генеральной сово­купности для интервала данных, предполагается известным;

• размер: размер выборки.

Математика-статистическая интерпретация: Одна из основных задач выборочного исследования состоит в том, чтобы на основе характеристик выборочной совокупности получить достоверные суждения об этих характеристиках в гене­ральной совокупности. Возможные расхождения между характе­ристиками выборочной и генеральной совокупности измеряются разностью между значением характеристики в генеральной сово­купности и ее значением, вычисленным по результатам выбороч­ного наблюдения. Для средней арифметической это расхождение определяется по формуле

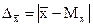
Зная выборочную среднюю величину признака и предель­ную ошибку выборки, можно определить границы, в которых заключена генеральная средняя.

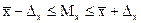
Интервал в котором заключена генеральная средняя получил название доверительного интервала.

Вероятность того, что случайный интервал содер­жит в себе истинное значение средней величины (генеральной средней), получила название доверительной вероятности.

Примечание. Необходимо отметить, что в качестве аргумента функция ДОВЕРИТ используется не доверительная вероятность, а уровень значи­мости.

Предельная ошибка выборки связана со средней ошибкой выборки через коэффициент доверия t

Средняя ошибка выборки определяется выражением:

,

где σ – стандартное отклонение, n – число наблюдений.

Коэффициент доверия определяется в зависимости от того, с какой доверительной вероятностью нужно гарантировать результаты выборочного обследования.

Если число наблюдений n > 30, то в Microsoft Excel для нахождения значения коэф­фициента доверия t можно использовать формулу t = НОРМСТОБР((γ + 1)/2), где γ -доверительная вероятность (см. опи­сание функции НОРМАЛИЗАЦИЯ, НОРМРАСП, НОРМОБР, НОРМСТРАСП, НОРМСТОБР), в противном случае необходимо использовать функцию СТЬЮДРАСПОБР(вероятность, степени_свободы). Здесь вероятность –это уровень значимости α, число степеней свободы – n-1.

Применение функции ДОВЕРИТ для решения практических задач рассмотрим на следующем примере.

Пример 3. В результате выборочного обследования жилищ­ных условий жителей города, осуществленного на основе собст­венно-случайной повторной выборки, получен следующий ряд распределения (табл. 4.1).

Таблица 4.1
Общая площадь	До 5	5-10	10-15	15-20	20-25	25-30	30 и более
Число жителей

Требуется с уровнем надежности 95% определить границы интервала, в который попадет средний раз­мер общей площади.

Таблица 4.2

Общая пло­щадь, прихо­дящаяся на 1 человека, м2	Середина интервала	Число жителей	Квадрат отклонения
До 5,0	2,5		272,42
5,0-10,0	7,5		132,37
10,0-15,0	12,5		42,32
15,0-20,0	17,5		2,27
20,0-25,0	22,5		12,22
25,0-30,0	27,5		72,17
30,0 и более	32,5		182,12
Число жителей в выбороч­ной совокупности, n
Выборочная средняя вариацион - ного ряда	19,01
Дисперсия σ2	51,11
Стандартное отклонение σ	7,15
Средняя ошибка выборки	0,23
Коэффициент доверия t	1,96
Предельная ошибка выборки Δx	0,44
Верхняя граница	19,45
Нижняя граница	18,56

3.2. ЗАДАНИЕ:

1) Проведено исследование величины ежемесячного среднедушевого дохода жителей поселка. Данные представлены в таблице 4.3.

Таблица 4.3.

№ интервала	Ежемесячный среднедушевой доход (д.е.)	Число жителей (чел.)
	70 - 80
	80 – 90
	90 – 100
	100 -110
	110 -120
	120 – 130
	130 – 140
	140 -150

1) Измените число жителей в таблице 4.3. в соответствии с вашим вариантом. Используя функцию НОРМРАСП необходимо определить, какой процент составляет среднедушевой доход 135 – 145 д.е.

2) Решите задачу примера 2, изменив значение стандартного отклонения в соответствии с вашим вариантом..

3) В таблице 4.1 измените число жителей в соответствии с вариантом задания и определите с вероятностью 90% верхнюю и нижнюю границы интервалов.

Рассмотрите два варианта решения задачи. Первый вариант основан на последовательном применении рассмотрен­ных формул для нахождения предельной ошибки выборки. Во втором варианте (более быстром) используйте функцию ДОВЕРИТ.

4) ИСПОЛЬЗОВАНИЕ КРИТЕРИЯ ПИРСОНА c² ДЛЯ ПРОВЕРКИ ГИПОТЕЗ