Метод Р.Гоморі

Р. Гоморі для отримання цілочисельних розв'язків розробив алгоритм, який використовує процедуру симплекс-методу. Він запропонував достатньо простий спосіб побудови правильної відтинаючої гіперплощини.

Суть цього методу полягає в тому, що спочатку задача лінійного програмування розв'язується без умови цілочисельності. Якщо отриманий розв'язок є цілочисельним, то задача розв'язана. В протилежному випадку до обмежень задачі додається ще одне, яке має такі властивості:

1) повинно бути лінійним;

2) повинно відтинати знайдений оптимальний нецілочисельний розв'язок;

3) не повинно відтинати жодного цілочисельного розв'язку.

Додаткове обмеження, яке має вказані властивості, називається правильною відтинаючою гіперплощиною.

Після цього отримана задача лінійного програмування розв'язується з врахуванням нового обмеження. Потім, якщо потрібно, додається ще одне відтинаюче обмеження і т.д. до отримання повністю цілочисельного розв'язку задачі.

Геометричне додавання додаткового лінійного обмеження відповідає проведенню гіперплощини, яка відтинає від многогранника планів деяку його частину разом з оптимальною точкою з нецілими координатами, але не зачіпає жодної із цілочисельних точок цього многогранника.

Припустимо, що в результаті розв'язування симплекс-методом канонічної задачі лінійного програмування (2.22)-(2.23) одержано оптимальний план (b ₁₀;… b_{k 0};… b_{m o};0;...;0), в яко­му, наприклад, b_{k 0} – неціла компонента. Нерівність

{ b_{k,m +1}} x_{m +l}+...+ { b_k,n } x_n ³ { b_{k 0}} (2.25)

сформована за k -им рядком, володіє всіма властивостями правильного відтинання.

Зауважимо, що в (2.25) присутній символ {...}, який означає дробову частину числа. А дробовою частиною { а } числа а, як відомо, називають різницю між цим числом і його цілою частиною [ а ] (найменшим цілим, яке не перевищує а).

Наприклад, якщо , то ; якщо а =–2,3, то {–2,3}=–2,3–[–2,3]=–2,3–(–3)=0,7.

Для розв'язування задачі цілочисельного лінійного програмування (2.22)–(2.24) використовують наступний алгоритм.

1. Симплекс-методом розв'язуємо задачу лінійного програмування (2.22)–(2.23). Якщо всі компоненти оптимального розв’язку цілі, то він є оптимальним і для задачі (2.22)–(2.24). Якщо задача (2.22)–(2.24) не має розв'язку, то і задача цілочисельного лінійного програмування також не має розв'язку. Якщо ж серед компонент оптимального розв’язку задачі (2.22)–(2.23) є нецілі компоненти, то переходимо до п.2.

2. Серед нецілих компонент вибираємо з найбільшою дробовою частиною та за відповідним рядком симплекс-таблиці, яка містить нецілочисельний оптимальний розв’язок, формуємо правильне відтинання (2.25).

3. Нерівність (2.25) введенням додаткової невід'ємної цілочисельної змінної перетворюємо в еквівалентне рівняння і включаємо його в симплекс-таблицю з нецілочисельним оптимальним розв’язком.

4. Одержану розширену задачу лінійного програмування розв'язуємо симплекс-методом. Якщо одержаний оптимальний розв’язок буде цілочисельним, то задача цілочисельного лінійного програмування (2.22)–(2.24) розв'язана. В іншому випадку повертаємося до п.2.

Якщо задача має розв'язок в цілих числах, то після скінченого числа повторів оптимальний цілочисельний розв’язок буде знайдений. Якщо ж в процесі розв'язування з'явиться рядок з нецілим вільним членом і рештою цілих коефіцієнтів, то відповідне рівняння не має розв'язку в цілих числах. В цьому випадку і дана задача не має цілочисельного оптимального розв’язку.

Приклад. Знайти максимум функції f =2 х ₁+3 х ₂ при обмеженнях

Розв'язок. Розв'язуючи задачу симплекс-методом, одержимо оптимальний розв’язок (Рис. 2.31).

За рядком змінної х ₁, яка набула нецілочисельне значення в оптимальному розв’язку, складаємо обмеження (2.25):

.

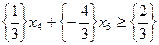	-1	-1

Рис. 2.31.

Ввівши додаткову цілочисельну змінну x ₆³0, одержимо її вираз через базисні змінні:

.

Доповнимо симплекс-таблицю ще одним рядком і одержимо наступну таблицю (Рис. 2.32):

	–1	–1

Рис. 2.32.

Повторивши процес розв'язування симплекс-методом стосовно розширеної задачі, одержимо оптимальний цілочисельний розв’язок Х =(2;7;19;0;1;0), f _max=25 (Рис. 2.33).

	–	–
		-2
	–
		–
			–25

Рис. 2.33.

? Контрольні запитання