Решение систем уравнений. Решение нелинейных уравнений

Решение систем линейных уравнений.

Рассмотрим методы решения системы линейных уравнений:

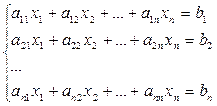(1)

Прямые методы

Правило Крамера. Одним из способов решения системы линейных уравнений является правило Крамера, согласно которому каждое неизвестное представляется в виде отношения определителей:

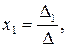
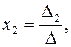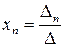…, , (2)

где D - определитель системы (1),

D_i – определители, полученные путем замены i-го столбца столбцом свободных членов системы (1).

Правило обратной матрицы. Известен также метод решения линейной системы с использованием обратной матрицы. Система записывается в матричном виде А * Х = В. Тогда, умножая обе части этого уравнения слева на обратную матрицу А ^-1, получаем Х = А^-1 * В.

Метод Гаусса. Наиболее распространенными среди прямых методов являются метод исключения Гаусса и его модификации. Он основан на приведении матрицы системы к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы. Сначала с помощью первого уравнения исключается x₂ из всех последующих уравнений системы. Затем с помощью второго уравнения исключается x ₃ из третьего и всех последующих уравнений. Этот процесс, называемый прямым ходом метода Гаусса, продолжается до тех пор, пока в левой части последнего (n-го) уравнения не останется лишь один член с неизвестным x_n, т.е. матрица системы будет приведена к треугольному виду.

Обратный ход метода Гаусса состоит в последовательном вычислении искомых неизвестных: решая последнее уравнение, находим единственное неизвестное x_n. Далее, используя это значение, из предыдущего уравнения вычисляем x_{n -1} и т.д. Последним найдем x₁ из первого уравнения.

Примеры решения систем линейных алгебраических уравнений прямыми методами даны в приложении А.