Тригонометрическая форма комплексных чисел

Запись комплексного числа Z в виде A+B· i называется алгебраической формой комплексного числа. Помимо алгебраической формы используются и другие формы записи комплексных чисел.

Рассмотрим тригонометрическую форму записи комплексного числа. Действительная и мнимая части комплексного числа Z=A+B· i выражаются через его модуль 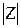= rи аргумент j следующим образом:

A= r·cosj; B= r·sinj.

Число Z можно записать так:

Z= r·cosj+ i · 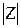·sinj = r·(cosj + i ·sinj)

Z = r·(cosj + i ·sinj) (2)

Эта запись называется тригонометрической формой комплексного числа.

r = 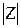– модуль комплексного числа.

Число j называют аргументом комплексного числа.

Аргументом комплексного числа Z 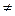0 называется величина угла между положительным направлением действительной оси и вектором Z, причем величина угла считается положительной, если отсчет ведется против часовой стрелки, и отрицательной, если производится по часовой стрелке.

Как уже говорилось выше 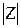= r = , равенство (2) можно записать в виде

A+B· i = · cosj + i · · sinj, откуда приравнивая действительные и мнимые части, получим:

cosj = , sinj =

Произведение комплексных чисел, записанных в тригонометрической форме, можно находить по формуле:

Z₁Z₂= r₁·r₂ [cos(j₁ + j₂) + i ·sin(j₁ + j₂)]

Вообще для любого комплексного числа Z = r·(cosj + i ·sinj) 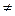0 и любого натурального числа n справедлива формула:

Zⁿ =[ r·(cosj + i ·sinj)]ⁿ= rⁿ·(cosnj+ i ·sinnj),

которую называют формулой Муавра.

Частное двух комплексных чисел, записанных в тригонометрической форме, можно находить по формуле:

Число Z называется корнем степени n из числа w (обозначается ), если Zⁿ =w.

все решения могут быть записаны следующим образом:

Z_K= [cos() + i ·sin()], kÎZ

Формулу называют второй формулой Муавра.

Основные понятия теории многочленов. Действия с многочленами.

Определение 1. Одночленом называется выражение, которое содержит числа, натуральные степени переменных, и их произведения и не содержит никаких других действий над числами.

Например, выражения 5х³0,4у, -3ab² 2/3xy⁵, -1,7х³у⁵а являются одночленами, а выражения 3с – а, 2ху/с одночленами не являются.

Введем понятие многочлена через алгебраическую сумму.

Определение 2. Алгебраическая сумма одночленов называется многочленом.

Например, 3х² +4х - 7, 5ma + 2x³ + 18 являются многочленами, тогда как выражения х у, a + b многочленами не являются.

х² + 3у⁴ – 8 3(x + y)

Введём следующие определения.

Определение 3. Подобными членами многочленов называются слагаемые, имеющие одинаковую буквенную часть.

Если в многочлене все одночлены записаны в стандартном виде и приведены подобные члены, то полученный многочлен называется многочленом стандартного вида.

А теперь дадим более широкое определение многочлена.

Определение 4. Многочлен с одной переменной х – это выражение вида

a₀xⁿ + a₁x^n-1+… a_n-1x + a_n, где n – любое натуральное число или 0, коэффициенты a₀, a₁, … a_n-1 , a_n – любые действительные числа. Выражения a₀xⁿ, a₁x^n-1, a_n-1x , a_n называют членами многочлена. Число n называется степенью многочлена. Коэффициент при наибольшем показателе степени х многочлена называется старшим коэффициентом многочлена f(x), а слагаемое, не содержащее х, называется свободным членом.

Определение 5. Степенью многочлена стандартного вида называется наибольшая степень одночлена, входящего в состав данного многочлена.