 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Найти пределы ( не пользуясь правилом Лопиталя)
|
|
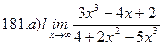
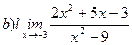
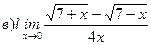
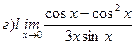
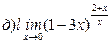
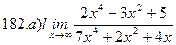
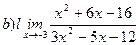
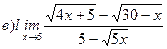
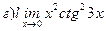
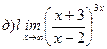
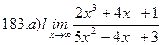
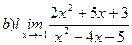
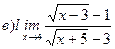
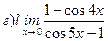
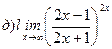
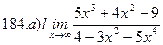
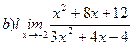
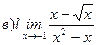
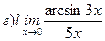
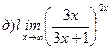
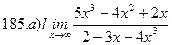
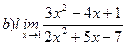
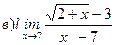
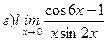
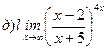
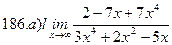
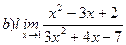
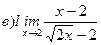
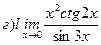
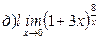
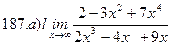
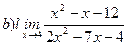
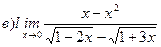
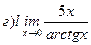
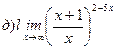
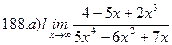
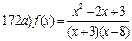
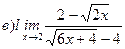
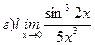
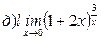
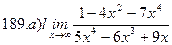
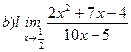
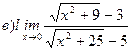
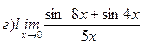 ∑
∑
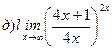
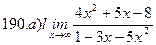
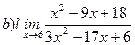
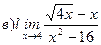
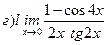
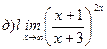
191-200. Дана функция y=f(x) и два значения аргумента х1 и х2. Установить, является ли данная функция непрерывной или разрывной для каждого из данных значений х. Построить приближенно график функции в окрестностях каждой из данных точек.
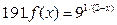
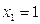
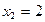
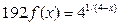
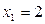
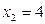
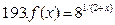
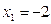
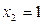
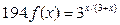
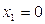
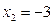
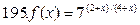
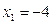
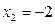
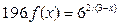
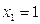
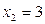
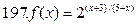
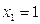
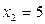
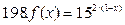
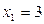
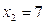
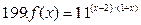
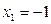
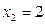
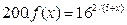
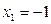
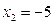
В задачах а) и б) найти точки разрыва функции. Определить характер разрыва, сделать чертеж.
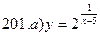
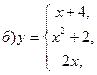
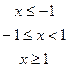
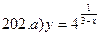
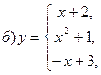
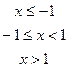
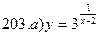
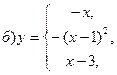
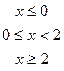
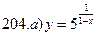
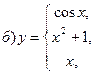
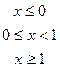
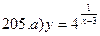
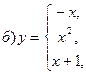
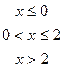
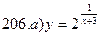
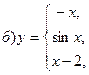
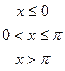
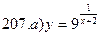
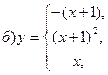
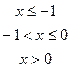
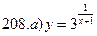
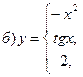
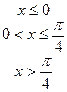
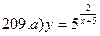
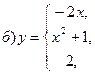
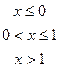
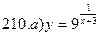
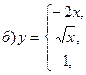
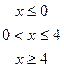
211-220. Найти производные 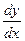 данных функций:
данных функций:
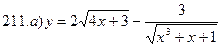
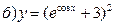
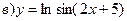
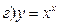
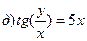
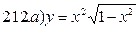
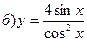
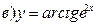
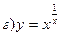
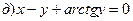
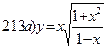
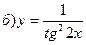
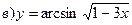
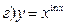
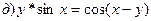
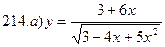
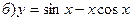
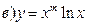
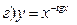
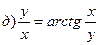
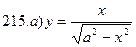
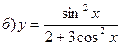
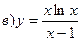
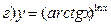
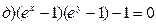
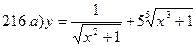
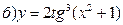
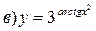
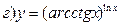
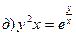
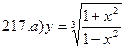
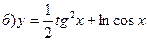
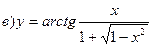
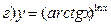
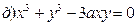
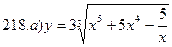
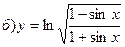
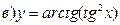
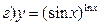
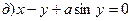
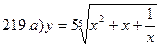
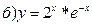
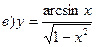
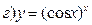
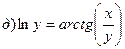
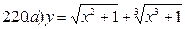
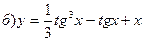
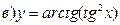
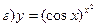
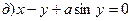
221-230. Найти 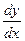 и
и 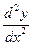 .
.
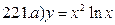
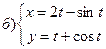
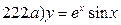
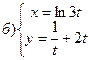
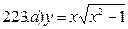
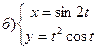
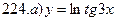
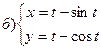
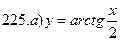
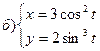
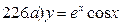
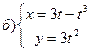
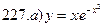
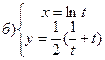
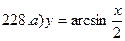
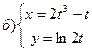
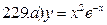
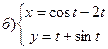
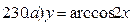
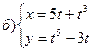
231-240. Найти наибольшее и наименьшее значения функции y=f(x) на отрезке [а; в].
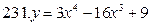 [-3;1]
[-3;1]
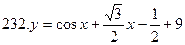 [0;
[0; 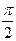 ]
]
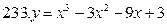 [-2;3]
[-2;3]
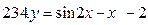 [
[ 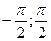 ]
]
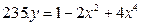 [-2;0]
[-2;0]
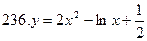 [
[ 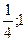 ]
]
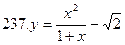 [-
[- 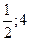 ]
]
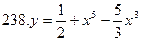 [0;2]
[0;2]
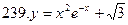 [-1;4]
[-1;4]
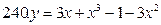 [-1;2]
[-1;2]
241-250. Исследовать методами дифференциального исчисления функцию y = f(x) и, используя результаты исследования, построить график.
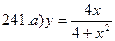
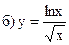
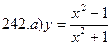
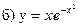
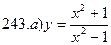
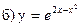
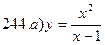
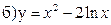
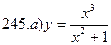
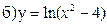
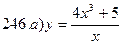
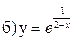
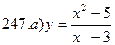
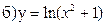
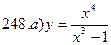
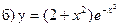
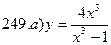
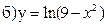
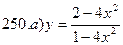
Дата публикования: 2015-09-18; Прочитано: 410 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
