Алгоритм методу Ленд-Дойга

1. Визначаються множини D (k;r) умовами (4.23), (4.24) i додатковими обмеженнями, які виникають в процесі розгалуження (див. пункт 5). На 0-у кроцi покладаємо D (0;1)= D, де D задається умовами (4.23), (4.24).

2. Розв’язуються допоміжні ЗЛП на множинах D (k;r). Нехай x (k;r) –оптимальні розв’язки вказаних ЗЛП.

3.Обчислюються границі на множинах D (k;r) за формулою (k;r)= ] L [ x (k;r)][, де ] z [ – найменше ціле число, не менше z.

4. Якщо існують k, l такі, що x (k;l) – дискретний розв’язок та для всіх гілок r на k -му кроцi виконуються співвідношення L [ x (k;l)] = (k;l) (k;r), то x * = x (k;l) – оптимальний розв’язок ДЗЛП.

5. Розгалуження здійснюється по недискретній компоненті xj (k;r) (з мінімальним j) розв’язку x (k;r), що відповідає перспективній гілці k;r (якщо таких гілок декілька, то вибирається гілка з мінімальним r), додаванням до D (k;r) однієї з пiдмножин x_j [ x_j (k;r)] або x_j [ x_j (k;r)] + 1.

Іншими словами, як і в методі Гоморі, процес починається з розв’я­зан­ня вихідної задачі. Якщо план X^* не задовольняє умову цілочисельності, то зна­чення цільової функції x=L (X) дає верхню оцінку шуканого розв’язку на множині планів G. Якщо деяка базисна змінна { x_l }- дробова, то в цілочисловому плані її слід зменшити до { x_l } або збільшити до{ x_l } +1. Тобто, вихідна множина G₀ розбивається на дві підмножини

Знаходимо розв’язки та оцінки на цих підмножинах. Якщо розв’язки на G⁽¹⁾₁, та G⁽²⁾₁, цілочислові, то оптимальним буде той, в якого оцінка x більша. Якщо ж, припустимо, що на множині G⁽¹⁾₁ маємо цілочисловий розв’язок, а на G⁽²⁾₁ - дробовий, але x (G⁽²⁾₁) > x  (G⁽¹⁾₁),то продовжуємо розбивати підмножину G⁽²⁾₁, оскільки на наступному кроці знайдемо цілочисловий план, оцінка яко­го буде більша від оцінки x (G⁽¹⁾₁). Цей процес продовжується до цілочислового розв’язку з максимальною оцінкою.

Приклад 4.2. Розв’язати методом гілок і границь задачі ЛП:

x₁ +2x₂ ® max,

2x₁ +2x₂ £ 7,

4x₁ –5x₂ £ 9,

x₁ ³ 0, x₂ ³ 0; де – х₁, х₂ – цілі.

Використовуючи геометричну інтерпретацію, на попередньому кро­ці знаходимо розв’язок вихідної ЗЛП без умов цілочисельності змін­них на множині планів задачі G₀ (рис. 4.1,а). Верхня оцінка x (G₀)  = 7, оптимальний план X^*₀ =( 0,7 / 2). Оскільки змінна x₂ – дробова, то у цілочисловому роз-в’язку її слід зменшити до 7/2 = 3 або збільшити до 7/2+ 1 = 4. На пер-шому кроці множина G₀ розбиваєтьсяна дві підмножини G⁽¹⁾₁ та G⁽²⁾₁, де:

Розв’язавши дві задачі ЛП на підмножинах G⁽¹⁾₁ та G⁽²⁾₁ (рис. 4.1,б), знайдемо: Х⁽¹⁾₁ =(1/2,3); x (G⁽¹⁾₁) = 13/2; G⁽²⁾₁= Æ; x (G⁽²⁾₁)= – ¥.

Розіб’ємо підмножину G⁽¹⁾₁ на G⁽¹⁾₂ та G⁽²⁾₂ (рис. 4.1, в), де

Розв’язуючи отримані таким чином ЗЛП дістаємо: Х⁽¹⁾₂ = (0,3); x (G⁽¹⁾₂) = 6; Х⁽²⁾₂ = (1,5/2); x (G⁽²⁾₂) = 6.

Оскільки на G⁽²⁾₂ змінна х₂ – дробова, то розбиваємо G⁽²⁾₂ на підмножини (рис. 4.1, г):

.

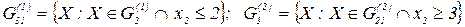З рис. 4.1,г дістаємо, що: Х⁽¹⁾₃ =(3/2,2); x(G⁽¹⁾₃) =11/2 < x(G⁽¹⁾₂). G⁽²⁾₃ =Æ. На цьому розв’язування цілочислової ЗЛП закінчено й тому робимо висновок, що X^* =(0,3), L(X^*) =6.

Рисунок 4.1

На рис. 4.1,в-г дано геометричну інтерпретацію розв’язання вихідної задачі, а на рис. 4.2 – дерево розв’язків.

Рисунок 4.2