Алгоритм методу Гоморi-1

1. Розв’язуємо допоміжну ЗЛП (4.1)(4.3). Нехай x (0) – її оптимальний розв’язок. Якщо оптимальний розв’язок не існує, то вихідна ДЗЛП також не має оптимального розв’язку.

2. Нехай на s -й iтерацiї маємо розв’язок допоміжної ЗЛП, що має M обмежень i N змінних, x (s) – її оптимальний розв’язок.

Будемо вважати, що x (s) визначається канонічними обмеженнями останньої iтерацiї, тобто:

x_i + b_i,M+1x_M+1+...+ b_iNx_N= b_i0, i=1,...,M,

звідки x (s) = (b₁₀,...,b_M0, 0 ,..., 0).

3. Якщо b_i0 (i=1,...,M) – цілі, то – кінець, x (s) є оптимальним розв’язком вихідної ДЗЛП. Якщо існує хоча б одне i таке, що b_i0 – дріб, то перехід до пункту 4.

4. Знаходимо r = min { i } за всіма i такими, що b_i0 – дріб та будуємо додаткове обмеження

x_N+1 – { b_r,M+1 } x_M+1 – ... – { b_rN } x_N= – { b_r0 },

де x_N+1 0 – додаткова змінна.

5. Розширюємо симплекс-таблицю (M+1)-им рядком (додаткове обмеження) та (N+1)-им стовпцем, що відповідає додатковій змінній x_N+1.

6. Розв’язуємо розширену таким чином ЗЛП двоїстим симплекс-мето­дом i переходимо до пункту 2 із заміною s на s+1. Якщо при цьому, на деякiй iтерацiї одна з додаткових змінних задачі повторно стає базисною, то виключаються з подальшого розгляду відповідні їй рядок i стовпець.

Приклад 4.1. Розв’язати цілочислову ЗЛП методом Гоморі-1:

x₁ +x₂ ® max,

6 x₁ + 5 x₂ £ 30,

x₂ £ 3,

x₁ ³ 0, x₂ ³ 0, де х₁ х₂ - цілі.

Відкидаючи умови цілочисельності змінних, на попередньому кроці знаходимо розв’язок задачі звичайним симплекс-методом (див. табл. 4.1).

Таблиця 4.1

i	Б	С	Х	1	1	0	0
P1	P2	P3	P4
	P3
	P4
m+1				-1	-1
	P1				5/6	1/6
	P4
m+1					-1/6	1/6
	P1		5/2			1/6	-5/6
	P2
m+1			11/2			1/6	1/6

Таблиця 4.2

і	Б	С	Х	1	1	0	0	0
P1	P2	P3	P4	P5
	P1		5/2			1/6	-5/6
	P2
	P5		-1/2			-1/6	-1/6
m+1			11/2			1/6	1/6

Таблиця 4.3

і	Б	С	Х	1	1	0	0	0
P1	P2	P3	P4	P5
	P1						-1
	P2
	P5							-6
m+1

Оскільки в оптимальному розв’язку змінна x₁ дробова, то виконаємо загальний крок алгоритму. Запишемо додаткове обмеження. Для цього знайдемо, що

Додаткове обмеження має вигляд: Зведемо його до канонічної форми запису: 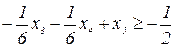і внесемо в останню симплекс-таблицю. Маючи табл. 4.2, і виконуючи один крок двоїстого симплекс-методу, приходимо до завершаль­ної табл. 4.3.

Розв’язок вихідної задачі дістаємо у вигляді X^* =(2, 3), L (X^*)=5.

Задача частково дискретного ЛП. Метод Гоморi-2

Постановка частково дискретної задачі ЛП (ЧДЗЛП). Знайти вектор x = (x₁,...,x_n), що мiнiмiзує цільову функцію

L (x) = c₁x₁+... + c_nx_n (4.5)

i задовольняє систему обмежень

a₁₁x₁ +... + a_1nx_n= a₁₀,

......................., (4.6)

a_m1x₁+... + a_mnxn = a_m0,

x_j0, j=1,...,n, (4.7)

x_j цілі, j=1,...,p, (pn). (4.8)

Виклад методу Гоморi-2. Метод Гоморi-2, як i метод Гоморi-1, є одним із методів відсікання його суть.

Розв’язується допоміжна ЗЛП (4.5) – (4.7), яку отримують з вихідної ЗЛП (4.5) – (4.8) відкиданням умови дискретності змінних (4.8). Якщо її розв’язок задовольняє умову (4.8), то він же є i розв’язком вихідної ЧДЗЛП. Інакше, від розв’язаної ЗЛП переходять до нової допоміжної ЗЛП приєднанням лінійного обмеження, яке задовольняє дискретні (у розумінні умов (4.8) розв’язки вихідної ЧДЗЛП, але не задовольняє отриманий недискретний розв’язок вихідної ЗЛП. Це додаткове обмеження визначає деяку відсічну площину i називається правильним вiдсіканням. Приєднання нових правильних вiдсікань здійснюється до тих пір, поки на деякому кроцi не буде отримано дискретний (у розумінні умов (4.8) розв’язок допоміжної задачі, який i є оптимальним розв’язком вихідної ЧДЗЛП. В методі Гоморi-2 правильне вiдсікання будується таким чином.

Нехай на останній iтерацiї симплекс-методу під час розв’язування допоміжної ЗЛП її непрямі обмеження набули вигляду:

x_i + Q_i,m+1x_m+1+...+ Q_inx_n= Q_i0, i=1,...,m,

i розв’язком допоміжної ЗЛП є вектор x = (Q₁₀,..., Q_m0, 0 ,..., 0).

Нехай існує номер r (rp) такий, що Qr0 – не цiле, i { z } – дробова частина z. Тоді правильне вiдсікання методу Гоморi-2 має вигляд:

x_n+1 D_r,m+1x_m+1... D_rnx_n = { Q_r0 }, (4.9)

де x_n+1 0 – додаткова змінна, та

(4.10)