Ітерація 3

a = 93,75, b = 116,25, x_m = 105; L = 116,25 – 93,75 = 22,5;

x₁ = 99,375, x₂ = 110,625; f (x₁) = 0,39 < f(105) = 25.

Таким чином, вилучається інтервал (105; 116,25). Новий інтервал невизначеності дорівнює (93,75; 105), його середня точка є 99,375 (точка х₁ на ітерації 3). Відзначимо, що за три ітерації початковий інтервал пошуку довжиною 90 зменшився до величини (90)(1/2)³ = 11,25.

Як видно з алгоритму, з кожних трьох значень цільової функції W, що обчислюються в інтервалі пошуку, надалі використовується тільки два з них, а третє не дає додаткової інформації і надалі не використовується. За методом золотого перерізу цільова функція обчислюється в точках інтервалу, розташованих таким чином, щоб кожне обчислене значення цільової функції давало б нову корисну інформацію.

Зменшення інтервалу методом золотого перерізу. Із наведеного вище обговорення методу виключення інтервалів (мінімаксних стратегій пошуку) можна зробити такі висновки.

1. Якщо кількість пробних точок приймається рівною двом, то їх слід розміщувати на однакових відстанях від середини інтервалу.

2. У відповідності із загальною мінімаксною стратегією пробні точки повинні розміщуватись у інтервалі по симетричній схемі таким чином, щоб відношення довжини підінтервалу, що вилучається, до величини інтервалу пошуку залишалось постійним.

3. На кожній ітерації процедури пошуку повинно обчислюватись лише одне значення функції у отримуваній точці.

Керуючись цими висновками, розглянемо симетричне розміщення двох пробних точок на початковому інтервалі одиничної довжини, яке показане на рисунку нижче (вибір одиничного інтервалу пояснюється міркуваннями зручності).

Пробні точки віддалені від граничних точок інтервалу на відстань . При такому симетричному розміщенні точок довжина інтервалу, що залишається після вилучення, завжди дорівнює незалежно від того, яке із значень функції у пробних точках виявилось меншим. Припустимо, що вилучається правий підінтервал. На нижченаведеному рисунку показано, що підінтервал, що залишився, довжини містить одну пробну точку, розміщену на відстані від лівої граничної точки.

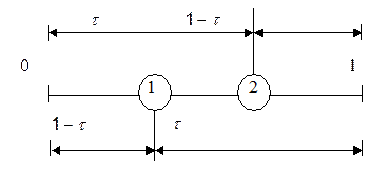
Для того, щоб симетрія пошуку зберігалась, відстань повинна складати – у частину довжини інтервалу, що дорівнює . При такому виборі наступна пробна точка розміщується на відстані, рівній - й частині довжини інтервалу, від правої граничної точки інтервалу. Звідси випливає, що за умови вибору з рівняння , симетрія пошуку буде зберігатися при переході до зменшеного інтервалу. Розв’язуючи це квадратне рівняння, отримаємо = (-1 ) /2, звідки додатний розв’язок = = 0,61803....

Схема пошуку, за якою пробні точки ділять інтервал у цьому відношенні, відома під назвою пошуку за допомогою методу золотого перерізу. Зауважимо, що після перших двох обчислень значень функції кожне наступне обчислення дозволяє виключити підінтервал, величина якого складає (1- )-у частину від довжини інтервалу пошуку. Отже, якщо початковий інтервал має одиничну довжину, то величина інтервалу, отриманого у результаті N обчислень значень функції, рівна ^N-1.

Можна показати, що пошук за допомогою методу золотого перерізу є асимптотично найбільш ефективним способом реалізації мінімаксної стратегії пошуку.

Приклад 5.3. Розглянемо задачу мінімізації функції f (x) = (100 - x)² на інтервалі .

Для того, щоб перейти до інтервалу одиничної довжини, в задачі, що розглядається, замість змінної x підставимо змінну . Виходячи з цього задача оптимізації буде мати вигляд

знайти мінімум функції

для обмежень .

Ітерація 1. Маємо . Проведемо два перших обчислення значення функції :

, ; , .

Виходячи з правила виключення інтервалів, оскільки та , інтервал виключається.

Ітерація 2. Маємо . Наступне обчислення значення функції проводиться при значенні змінної:

, .

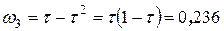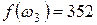Оскільки , а , вилучається інтервал .

Ітерація 3. . Наступне значення функції обчислюється для точки, яка знаходиться на відстані помножити на довжину отриманого інтервалу від лівої граничної точки інтервалу чи на відстані помножити на довжину отриманого інтервалу від правої граничної точки. Звідси:

.

Оскільки 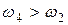, а , вилучається інтервал .

Таким чином ми отримали інтервал для змінної або інтервал для змінної х.

Якщо в процесі пошуку провести шість обчислень значень функції, то довжина отриманого інтервалу для змінної буде дорівнювати , що відповідає інтервалу довжини 8,1 для змінної х. Для порівняння нагадаємо, що в аналогічній ситуації для методу поділу інтервалу навпіл інтервал невизначеності дорівнював би 11,25.

У загальному випадку якщо права (XR) та ліва (XL) граничні точки інтервалу невизначеності відомі, то координати всіх наступних точок наближення згідно з методом золотого перерізу можуть бути обчислені за формулами або відповідно тому, який підінтервал був виключений на попередній ітерації – лівий або правий. У наведених формулах n – кількість обчислень значень фукції . Пошук закінчується, коли відносна точність оптимального значення змінної досягає деякого наперед заданого значення.

Зауваження. Якщо f (x₁) = f (x₂), то можна вилучити обидва крайні інтервали (a, x₁) та (x₂, b); при цьому точка мінімуму повинна розміщуватись у інтервалі (x₁, x₂).

Метод випадкового пошуку. Метод випадкового пошуку застосовується для знаходження мінімуму (максимуму) довільної функції y = F (x), що задана в будь-якiй допустимій області D.

Довiльна функція F (x) задана на проміжку [ A,B ]. За допомогою давача випадкових чисел, рівномірно розподілених на проміжку [ 0,1 ], будується послідовність випадкових чисел x { k }, k=1,...,N, рівномірно розподілених на проміжку [ A,B ]. Обчислюються та порівнюються між собою значення функції F (x) в точках x { k }. Мiнiмальне з них приймається за оцінку мінімуму функції F (x) на проміжку [ A,B ].

Якщо N прямує до нескінченності, отримана оцінка за ймовірністю збігається до глобального мінімуму функції, що розглядається.

При розв’язуванні задачі максимiзацiї функції F (x) необхідно замінити її на функцію – F (x).

Метод Фiбоначчi. Метод Фiбоначчi (МФ) застосовується для пошуку мінімуму унiмо­даль­ної функції однієї змінної y = F (x), що задана на проміжку [ A,B ].

Алгоритм методу реалізується у вигляді послідовності кроків, на кожному з яких здійснюється звуження інтервалу, що містить точку мінімуму.

На початку обчислень покладають A { 0 } = A, B { 0 } = B.

На s -у кроцi визначають величини

L { s } = B { s } – G { s } (B { s } – A { s }),

R { s } = A { s } + G { s } (B { s } – A { s }),

де G { s } =Fi (N – s – 1) Fi (N – s), s=0,...,N – 3, G { N – 2 } = (1+) 2 або (1 –) 2, N – задане число iтерацiй, > 0, Fi (j) – числа Фiбоначчi, що задаються рекурентним співвідношенням

Fi (j) = Fi (j – 1) + Fi (j – 2), j 2, Fi (0) = Fi (2.1) = 1.

Покладають

A { s+1 } = A { s }, B { s+1 } = R { s }, якщо F (L { s }) F (R { s }),

A { s+1 } = L { s }, B { s+1 } = B { s }, якщо F (L { s }) > F (R { s }).

За наближений розв’язок задачі приймають

x* = (A { N } + B { N }) 2, y* = F (x*).

Для МФ у випадку заздалегідь фіксованого числа iтерацiй довжина кін-цевого інтервалу пошуку мінімальна.