 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вектор прискорення точки
|
|
Величина, яка характеризує бистроту зміни швидкості точки з плином часу (як за модулем, так і за напрямком), називається прискоренням точки.
 Прискорення – величина векторна.
Прискорення – величина векторна.
Нехай точка, яка рухається по криволінійній траєкторії, в момент часу t займає на траєкторії положення М і має швидкість 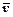 , а в момент t1 – положення М1 і швидкість
, а в момент t1 – положення М1 і швидкість  (рис.7). Визначимо приріст швидкості
(рис.7). Визначимо приріст швидкості  за проміжок часу
за проміжок часу  . Для цього вектор
. Для цього вектор  перенесемо в точку М. Сполучивши кінці векторів
перенесемо в точку М. Сполучивши кінці векторів 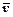 та
та  , отримаємо
, отримаємо  . Зауважимо, що вектор
. Зауважимо, що вектор  завжди напрямлений у бік угнутості траєкторії.
завжди напрямлений у бік угнутості траєкторії.
Відношення приросту вектора швидкості до проміжку часу ∆t визначає вектор середнього прискорення точки за цей проміжок часу:
 .
.
Напрямок вектора  , як видно, збігається з напрямком
, як видно, збігається з напрямком  .
.
Прискоренням точки в даний момент часу називається векторна величина  , до якої прямує середнє прискорення
, до якої прямує середнє прискорення  з наближенням проміжку часу Δt до нуля:
з наближенням проміжку часу Δt до нуля:
 або
або  .
.
Отже, вектор прискорення точки в даний момент часу дорівнює першій похідній від вектора швидкості або другій похідній від радіуса-вектора точки за часом.
Визначимо напрямок вектора  по відношенню до траєкторії руху точки. Якщо точка рухається прямолінійно, то вектор прискорення
по відношенню до траєкторії руху точки. Якщо точка рухається прямолінійно, то вектор прискорення  напрямлений вздовж прямої, по якій вона рухається, що очевидно. Якщо траєкторією руху є плоска крива, то вектор прискорення
напрямлений вздовж прямої, по якій вона рухається, що очевидно. Якщо траєкторією руху є плоска крива, то вектор прискорення  , як і
, як і  , лежить у площині цієї кривої і напрямлений у бік її угнутості. У загальному ж випадку вектор
, лежить у площині цієї кривої і напрямлений у бік її угнутості. У загальному ж випадку вектор  лежить у стичній площині й напрямлений у бік угнутості кривої.
лежить у стичній площині й напрямлений у бік угнутості кривої.
Питання для самоконтролю
1. Що вивчає розділ “Кінематика”?
2.Дати означення початковому моменту часу, даному моменту та проміжку часу.
3.Чим відрізняються поняття “відстань” та “шлях”? Коли відстань збігається зі шляхом?
4.Що таке траєкторія руху точки, кількість ступенів вільності точки або тіла?
5. У чому полягає головне завдання кінематики?
6. Які існують способи задання руху точки? Їх сутність.
7. Зв’язок координатного та векторного способів задання руху.
8.Що називається середньою швидкістю точки за проміжок часу Δt? Який напрямок вона має?
9. Дати означення вектору швидкості в даний момент часу. Його напрямок. Чому він дорівнює?
10. Що називається середнім прискоренням точки за проміжок часу Δt? Як воно напрямлене?
11.Дати означення вектору прискорення в даний момент часу. Його напрямок. Формули визначення.
Лекція № 11
Тема: “Визначення швидкості та прискорення точки при різних способах задання її руху”
План
1. Визначення швидкості й прискорення точки при координатному способі задання її руху.
2. Визначення швидкості й прискорення точки при натуральному способі задання руху.
3. Деякі поодинокі випадки руху точки.
1. Визначення швидкості й прискорення точки при координатному способі задання її руху
Як відомо, вектор швидкості точки визначається першою похідною від радіуса-вектора за часом:
 .
.
Але відповідно за формулою
 ,
,
де орти  ,
,  ,
,  – сталі як за модулем, так і за напрямком.
– сталі як за модулем, так і за напрямком.
Тоді:

Якщо визначити вектор швидкості  через його проекції на координатні осі, то дістанемо:
через його проекції на координатні осі, то дістанемо:

Порівнюючи ці вирази, помічаємо, що:

Таким чином, проекції вектора швидкості точки на осі координат дорівнюють першим похідним від відповідних координат точки за часом.
Знайдемо модуль і напрямок вектора швидкості за формулами:
 ;
;

Аналогічно визначається прискорення точки:

Звідси знайдемо проекції вектора прискорення та координатні осі:

Отже, проекції вектора прискорення точки на координатні осі дорівнюють першимпохідним від проекцій вектора швидкості або другим похідним від відповідних координат точки за часом.
Модуль і напрямок прискорення визначаються за формулами:


2. Визначення швидкості й прискорення точки при натуральному способі задання руху
Нехай задана траєкторія і закон руху точки у вигляді s = f(t).
 Точка за проміжок часу Δt перемістилася з положення М у положення М1 (рис.1). При цьому переміщення становить Δs=s1–s. Визначимо числову величину її середньої швидкості:
Точка за проміжок часу Δt перемістилася з положення М у положення М1 (рис.1). При цьому переміщення становить Δs=s1–s. Визначимо числову величину її середньої швидкості:
 .
.
Щоб знайти числову величину швидкості в даний момент часу t, перейдемо за границі:

Отже, числова величина швидкості в даний момент часу дорівнює першій похідній від відстані (криволінійної координати) s точки за часом.
 Вектор швидкості напрямлений по дотичній до траєкторії точки, причому, якщо v>0, то в додатному напрямку відліку відстані, а якщо v<0, то у від'ємному.
Вектор швидкості напрямлений по дотичній до траєкторії точки, причому, якщо v>0, то в додатному напрямку відліку відстані, а якщо v<0, то у від'ємному.
Вектор прискорення при натуральному способі задання руху визначається проекціями, але не на координатні осі системи відліку Оxyz, а на рухомі осі Мτnb, які мають початок у точці М і рухаються разом з нею (рис.2,б). Ці осі називають осями натурального тригранника. Вісь Мτ (дотична) напрямлена по дотичній до траєкторії руху точки в бік додатного відліку відстані, вісь Мn (головна нормаль) – по нормалі, яка лежить у стичній площині, й напрямлена в бік угнутості кривої, вісь Мb (бінормаль) – перпендикулярна двом попереднім. Як було показано в попередній лекції, вектор прискорення лежить у стичній площині, тому його проекція на бінормаль дорівнює нулю. Визначимо його проекції на дві інші осі. Проектуючи обидві частини рівності  на осі Мτ та Мn і позначаючи символами
на осі Мτ та Мn і позначаючи символами  та
та  проекції вектора
проекції вектора  на ці осі, дістанемо:
на ці осі, дістанемо:

Вектор  – це різниця між швидкостями в двох сусідніх точках М і М1, тобто
– це різниця між швидкостями в двох сусідніх точках М і М1, тобто  Відкладемо вектори
Відкладемо вектори  і
і 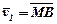 від спільної точки (рис.2,а). Тоді
від спільної точки (рис.2,а). Тоді  , а фігуру АСВD при нескінченно малому куті dφ можна розглядати як прямокутник. Звідси:
, а фігуру АСВD при нескінченно малому куті dφ можна розглядати як прямокутник. Звідси:

де dv – елементарний приріст числового значення швидкості.
Оскільки границя відношення дуги до хорди дорівнює одиниці, можна АD розглядати як елементарну дугу радіуса МА, розмір якої визначається добутком радіуса на центральний кут. Тоді:
 .
.
Підставляючи визначені значення  і
і  у рівняння, маємо:
у рівняння, маємо:

Кут між дотичними до кривої в двох її точках називається кутом суміжності, тоді dφ – елементарний кут суміжності.
Відношення dφ до  визначає кривизну кривої в точці М, а кривизна k є величиною, оберненою до радіуса кривизни ρ у цій точці, тобто:
визначає кривизну кривої в точці М, а кривизна k є величиною, оберненою до радіуса кривизни ρ у цій точці, тобто:

тому:
 .
.
Отже, остаточно маємо:
 .
.
Отже, проекція вектора прискорення точки на дотичну вісь дорівнює першій похідній від числової величини швидкості або другій похідній від відстані (криволінійної координати) s за часом, а проекція вектора прискорення на головну нормаль дорівнює квадрату швидкості, поділеному на радіус кривизни траєкторії в даній точці кривої.
Повне прискорення визначимо як геометричну суму складових (рис.3):
 .
.
 Рис.3
Рис.3
|
Перший доданок у рівнянні називається дотичним прискоренням, а другий – нормальним. Вектор  напрямлений завжди в бік угнутості кривої (величина
напрямлений завжди в бік угнутості кривої (величина  завжди додатна), а
завжди додатна), а 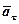 може бути напрямлений або в додатному, або у від'ємному напрямку осі Мτ, що залежить від знака проекції
може бути напрямлений або в додатному, або у від'ємному напрямку осі Мτ, що залежить від знака проекції 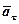 . Оскільки вектор нормального прискорення
. Оскільки вектор нормального прискорення  напрямлений до центра кривизни траєкторії, то його ще називають доцентровим.
напрямлений до центра кривизни траєкторії, то його ще називають доцентровим.
Модуль повного прискорення обчислюється так:

Відхилення вектора прискорення  від нормалі Мn характеризується кутом α, який визначається за формулою:
від нормалі Мn характеризується кутом α, який визначається за формулою:
 .
.
3. Деякі поодинокі випадки руху точки
Розглянемо деякі поодинокі випадки руху матеріальної точки.
1. Прямолінійний рух. Якщо траєкторією точки є пряма лінія, то ρ=∞, тоді  , і повне прискорення точки дорівнює одному тільки дотичному прискоренню:
, і повне прискорення точки дорівнює одному тільки дотичному прискоренню:
 .
.
Оскільки в цьому випадку швидкість змінюється тільки чисельно, то звідси робимо висновок, що дотичне прискорення характеризує зміну числового значення швидкості.
2. Рівномірний криволінійний рух. Рівномірним називається такий криволінійний рух точки, в якому числове значення швидкості весь час залишається сталим (v=const). Тоді  ,і повне прискорення дорівнює одному тільки нормальному прискоренню:
,і повне прискорення дорівнює одному тільки нормальному прискоренню:

Вектор прискорення  напрямлений при цьому весь час по нормалі до траєкторії точки.
напрямлений при цьому весь час по нормалі до траєкторії точки.
Оскільки в цьому випадку прискорення з'являється тільки за рахунок зміни напрямку швидкості, то звідси робимо висновок, що нормальне прискорення характеризує зміну швидкості за напрямком.
Знайдемо закон рівномірного криволінійного руху. Із формули  маємо: ds=vdt. Нехай у початковий момент часу (t0=0) точка знаходиться від початку відліку на відстані s0. Тоді:
маємо: ds=vdt. Нехай у початковий момент часу (t0=0) точка знаходиться від початку відліку на відстані s0. Тоді:

Або враховуючи, що v=const, дістанемо:
s-s0=vt,
звідси маємо:
s=s0+vt.
Якщо s0=0, то s дасть шлях, пройдений точкою за час t. Отже, при рівномірному русі шлях, пройдений точкою, зростає пропорційно часу, а швидкість точки дорівнює відношенню шляху до часу:
 .
.
3. Рівномірний прямолінійний рух. У цьому випадку an=aτ=0, а отже, a=0. Це єдиний рух, в якому прискорення точки весь час дорівнює нулю.
4. Рівнозмінний криволінійний рух. Рівнозмінним називається такий криволінійний рух точки, в якому дотичне прискорення залишається весь час сталим: aτ= const. Знайдемо закон цього руху, якщо відомо, що в початковий момент часу t0=0: s=s0, а v=v0 (s0 та v0 – початкові відстань та швидкість).
Оскільки dv=aτdt, а aτ=const, то беручи інтеграли з обох частин у відповідних границях, маємо:
v=v0+aτt
або
 ,
,
звідки:
ds=v0dt+ aτtdt.
Якщо ще раз проінтегруємо останню рівність, знайдемо закон рівнозмінного криволінійного руху точки:

Ці формули виражають також закон рівнозмінного прямолінійного руху точки, якщо вважати s=x. При цьому в рівняннях aτ=а, де а – числове значення прискорення даної точки.
5. Гармонійні коливання. Гармонійні коливання точки відбуваються за законом
x=Acos kt,
де А, k – сталі величини.
Величина А, яка дорівнює найбільшому відхиленню точки від центра коливань, називається амплітудою коливань.
Проміжок часу Т=2π/k, за який точка здійснює одно повне коливання, називається періодом коливань.
Беручи похідні від х за часом, знайдемо швидкість і прискорення точки:
v= – Aksin kt; a= – Ak2cos kt.
Питання для самоконтролю
1.Як визначається величина та напрямок швидкості точки при координатному способі задання її руху?
2.Як визначається прискорення точки при координатному способі задання її руху?
3.Як визначається швидкість при натуральному способі задання руху точки?
4.Як визначається прискорення точки при натуральному способі задання її руху?
5.Якими формулами описуються прямолінійний, рівномірний криволінійний, рівномірний прямолінійний та рівнозмінний криволінійний рухи?
Лекція № 12
Тема: “Поступальний і обертальний рухи твердого тіла”
План
1. Поступальний рух твердого тіла.
2.Обертальний рух твердого тіла. Кутові швидкість та прискорення.
3. Швидкості й прискорення точок тіла, яке обертається навколо осі.
1. Поступальний рух твердого тіла
У кінематиці всі тверді тіла будемо розглядати як абсолютно тверді, тобто такі, в яких відстані між двома будь-якими точками тіла залишаються сталими за весь час руху.
Завдання кінематики твердого тіла розкладається на дві частини:
1) задання руху і вивчення кінематичних характеристик руху всього тіла в цілому;
 2) вивчення руху кожної точки тіла окремо.
2) вивчення руху кожної точки тіла окремо.
Поступальним називається такий рух твердого тіла, при якому будь-яка пряма, проведена в цьому тілі, рухається паралельно сама собі.
Поступальний рух не слід плутати з прямолінійним. На відміну від останнього, де траєкторією руху є пряма, в поступальному русі траєкторіями точки тіла можуть бути будь-які криві. Прикладом поступального руху є рух шатуна АВ у чотириланковому механізмі О1АВО2 (рис.1), який складається з двох кривошипів О1А та О2В однакової довжини і шатуна АВ, довжина якого дорівнює відстані О1О2. Очевидно, що в усіх положеннях механізму чотирикутник О1АВО2 залишається паралелограмом. Отже, шатун АВ весь час паралельний прямій О1О2, і його рух є поступальним.
Теорема про траєкторії, швидкості й прискорення в поступальному русі. У поступальному русі всі точки тіла описують однакові (такі, що при накладанні збігаються) траєкторії і мають у кожний момент часу однакові за модулем і напрямком швидкості та прискорення.
 Доведення. Розглянемо тіло, яке здійснює поступальний рух відносно обраної системи відліку Охуz. Візьмемо в ньому довільні точки А і В, положення яких у момент часу t визначається відповідними радіусами-векторами
Доведення. Розглянемо тіло, яке здійснює поступальний рух відносно обраної системи відліку Охуz. Візьмемо в ньому довільні точки А і В, положення яких у момент часу t визначається відповідними радіусами-векторами  і
і  (рис.2). Провівши вектор
(рис.2). Провівши вектор  , помічаємо, що
, помічаємо, що

Оскільки відстань між точками твердого тіла – величина стала, то довжина АВ залишається однаковою в усіх його положеннях, напрямок  не змінюється, тому що тіло рухається поступально. Таким чином, вектор
не змінюється, тому що тіло рухається поступально. Таким чином, вектор  за весь час руху залишається сталим.
за весь час руху залишається сталим.
Отже, при поступальному русі тіла радіуси-вектори двох його довільних точок, змінюючись, будуть відрізнятися один від одного на сталий вектор. Тому траєкторії точок А і В будуть однаковими, вони збігаються одна з одною при паралельному їх перенесенні.
Продиференціюємо отримане рівняння за часом, маємо:
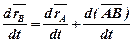 .
.
Похідна від сталого вектора  дорівнює нулю. Похідні від векторів
дорівнює нулю. Похідні від векторів  та
та  за часом дають швидкості відповідних точок. Тому
за часом дають швидкості відповідних точок. Тому
 ,
,
тобто швидкості двох точок тіла А і В у будь-який момент часу при поступальному русі однакові як за модулем, так і за напрямком. Тепер продиференціюємо отриману рівність за часом, дістанемо:
 або
або  ,
,
тобто прискорення точок А і В тіла у будь-який момент часу його руху також однакові за модулем і напрямком. Теорема доведена.
З теореми випливає, що поступальний рух цілком визначається рухом якої-небудь його точки. Тому завдання вивчення поступального руху зводиться до завдань кінематики точки, які розглянуті вище.
При поступальному русі спільну для всіх точок тіла швидкість  називають швидкістю поступального руху тіла, а прискорення
називають швидкістю поступального руху тіла, а прискорення  – прискоренням поступального руху тіла. Вектори
– прискоренням поступального руху тіла. Вектори  і
і  можуть бути зображені прикладеними в будь-якій точці тіла.
можуть бути зображені прикладеними в будь-якій точці тіла.
Зауважимо, що говорити про швидкість і прискорення тіла можна тільки у випадку його поступального руху, в інших випадках точки тіла мають різні швидкості й прискорення.
2. Обертальний рух твердого тіла. Кутові швидкість і прискорення
 Обертальним називається такий рух твердого тіла, в якому які-небудь дві точки, взяті на тілі (або незмінно з ним зв'язані), залишаються весь час нерухомими (рис.3). Пряма ОО1, яка з'єднує нерухомі точки О і О1, називається віссю обертання. Всі точки, які лежать на осі обертання, будуть нерухомими, а решта − описують кола з центром на осі обертання, причому площини кіл будуть перпендикулярні до осі обертання.
Обертальним називається такий рух твердого тіла, в якому які-небудь дві точки, взяті на тілі (або незмінно з ним зв'язані), залишаються весь час нерухомими (рис.3). Пряма ОО1, яка з'єднує нерухомі точки О і О1, називається віссю обертання. Всі точки, які лежать на осі обертання, будуть нерухомими, а решта − описують кола з центром на осі обертання, причому площини кіл будуть перпендикулярні до осі обертання.
Прикладом обертального руху може бути рух дверей або створок вікон при їх відкриванні, рух стрілок годинника, обертання ротора електродвигуна тощо.
Нехай деяке тіло обертається навколо осі ОО1 (рис.3). Проведемо через вісь обертання в деякий момент часу площину S і зафіксуємо її положення в просторі, а через певний проміжок часу проведемо площину S1, незмінно зв'язану з тілом. Кут φ між цими площинами, взятий з відповідним знаком, буде визначати положення тіла в будь-який момент часу. Кут φ називається кутом повороту тіла. Умовимось, що додатний напрям кута φ буде в тому випадку, якщо поворот площини S1 відносно фіксованої площини S здійснився проти ходу годинникової стрілки (дивитися слід з боку додатного напрямку осі Оz), і від'ємним – за ходом годинникової стрілки. Кут φ вимірюється в радіанах.
Щоб визначити положення тіла в просторі в будь-який момент часу, необхідно знати залежність між кутом повороту φ і часом t, тобто:
φ=f(t).
Це рівняння називається рівнянням обертального руху тіла.
Бистрота зміни кута повороту з часом характеризується величиною, яка називається кутовою швидкістю.
За достатньо малий проміжок часу Δt кут змінюється на величину Δφ. Відношення Δφ до Δt називається середньою кутовою швидкістю за даний проміжок часу і позначається ωср:
ωср.=  .
.
Кутовою швидкістю в даний момент часу t називається величина, до якої прямує значення ωср, коли проміжок часу Δt наближається до нуля:
 .
.
Таким чином, кутова швидкість у даний момент часу чисельно дорівнює першій похідній від кута повороту за часом, тобто показує, на який кут повертається тіло за одиницю часу. Кутова швидкість визначає також і напрямок обертання. Так, якщо ω>0, то тіло обертається в напрямку збільшення кута повороту – проти ходу годинникової стрілки, і в зворотному напрямку, якщо ω<0. Кутова швидкість вимірюється в радіанах за секунду (рад/с, с-1).
Якщо ω=соnst, то обертання тіла називається рівномірним. Закон рівномірного обертання: φ=φ0+ωt. Якщо φо=0, то φ=ωt.
Звідси кутова швидкість обчислюється за формулою:
 .
.
У техніці швидкість рівномірного обертання часто задають числом n обертів за хвилину. Знайдемо між ними залежність. За один оберт тіло повертається на кут 2π, а за n обертів – на 2πn. Цей поворот виконується за час t=1хв=60с, тоді маємо:
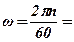
 .
.
Кутову швидкість зображають у вигляді вектора  , який напрямлений вздовж осі обертання в той бік, звідки обертання тіла відбувається проти ходу годинникової стрілки (див. рис.3).
, який напрямлений вздовж осі обертання в той бік, звідки обертання тіла відбувається проти ходу годинникової стрілки (див. рис.3).
Кутове прискорення характеризує бистроту зміни швидкості з часом. За проміжок часу ∆t швидкість тіла змінюється на ∆ω. Відношення ∆ω до ∆t називається середнім кутовим прискоренням за цей проміжок часу і позначається εср:
 .
.
Кутовим прискоренням в даний момент часу t називається величина, до якої прямує εср ., коли проміжок часу Δt наближається до нуля:

або, зваживши на попередній результат, маємо:

Таким чином, кутове прискорення в даний момент часу чисельно дорівнює першій похідній від кутової швидкості або другій похідній від кута повороту тіла за часом, тобто показує зміну кутової швидкості за одиницю часу. Кутове прискорення вимірюється в радіанах за секунду в квадраті (рад/с2, с-2).
Якщо знаки ω і ε однакові, то рух прискорений, якщо різні – сповільнений.
Якщо за час руху ε залишається сталою величиною, то такий рух називається рівнозмінним. Знайдемо закон рівнозмінного обертання. Для цього оберемо початковий момент часу t0=0, кут φ=φ0, а початкова швидкість ωо.
Знаючи, що  , дістанемо:
, дістанемо:
dω=εdt.
Проінтегруємо ліву частину в межах від ωо до ω, а праву −вмежах від 0 до t, дістанемо:

Це рівняння запишемо у вигляді:
 .
.
Проінтегруємо другий раз і маємо закон рівнозмінного обертання:
 .
.
Кутове прискорення тіла, як і кутову швидкість, зображають у вигляді вектора  , який напрямлений вздовж осі обертання, причому його напрямок збігається з напрямком
, який напрямлений вздовж осі обертання, причому його напрямок збігається з напрямком  уприскореному русі й протилежний – у сповільненому.
уприскореному русі й протилежний – у сповільненому.
3. Швидкості й прискорення точок тіла, яке обертається навколо осі
Точки тіла, яке обертається навколо осі, рухаються не однаково. Але, знаючи закон обертального руху тіла, можна визначити швидкість і прискорення будь-якої його точки в будь-який момент часу. З цією метою встановимо залежність між кутовими величинами φ, ω та ε, які характеризують обертальний рух тіла, і лінійними величинами s, v, а τ, an, а, які характеризують рух точок тіла.
Як ми відзначили вище, точки тіла, що обертається, рухаються по колах, центри яких лежать на осі обертання.
Нехай точка А тіла (рис.4), яке нерівномірно обертається навколо осі О, з поворотом його на кут φ пройде відстань s. Вона вимірюється дугою  кола, радіус якого R. Тоді:
кола, радіус якого R. Тоді:
s=Rφ.
 Відстань s і кут φ – функції часу t, а R – величина стала для даної точки. Продиференціюємо за часом обидві частини рівняння і дістанемо:
Відстань s і кут φ – функції часу t, а R – величина стала для даної точки. Продиференціюємо за часом обидві частини рівняння і дістанемо:
 або v = R ω.
або v = R ω.
Швидкість ν називається лінійною або коловою швидкістю точки А.
Таким чином, лінійна швидкість точки твердого тіла, яке обертається навколо осі, чисельно дорівнює добутку кутової швидкості тіла на відстань від цієї точки до осі обертання.
 Лінійна швидкість напрямлена по дотичній, проведеній до кола, описуваного точкою А, або перпендикулярно до радіуса R. Оскільки ω для всіх точок тіла в даний момент має одне й те ж значення, то із формули випливає, що лінійні швидкості точок тіла, яке обертається навколо осі, пропорційні їх відстаням від осі обертання.
Лінійна швидкість напрямлена по дотичній, проведеній до кола, описуваного точкою А, або перпендикулярно до радіуса R. Оскільки ω для всіх точок тіла в даний момент має одне й те ж значення, то із формули випливає, що лінійні швидкості точок тіла, яке обертається навколо осі, пропорційні їх відстаням від осі обертання.
Покажемо, що вектор лінійної швидкості точки тіла, що обертається, можна визначити як векторний добуток кутової швидкості тіла на радіус-вектор точки, проведений із довільної точки О, взятої на осі обертання (рис.5), тобто
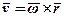 .
.
Ця формула називається формулою Ейлера. Отже, необхідно довести, що вектор ( ) напрямлений по дотичній до траєкторії точки в бік обертання тіла, амодуль його дорівнює модулю швидкості точки М, тобто
) напрямлений по дотичній до траєкторії точки в бік обертання тіла, амодуль його дорівнює модулю швидкості точки М, тобто
׀  ׀ = ωR.
׀ = ωR.
Дійсно, векторний добуток  дає вектор, перпендикулярний площині, в якій лежать вектори
дає вектор, перпендикулярний площині, в якій лежать вектори  i
i 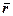 (це площина ОМС), напрямлений у той бік, звідки найкоротший поворот від вектора
(це площина ОМС), напрямлений у той бік, звідки найкоротший поворот від вектора  до вектора
до вектора 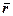 бачиться проти ходу годинникової стрілки. Цей напрямок збігається з напрямком вектора
бачиться проти ходу годинникової стрілки. Цей напрямок збігається з напрямком вектора  . При цьому
. При цьому
׀  ׀ = ׀
׀ = ׀  ׀·׀
׀·׀ 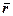 ׀ sinβ,
׀ sinβ,
де β – кут між векторами  i
i 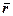 .
.
Як бачимо з рисунка, ׀ 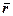 ׀ sinβ = R, тоді ׀
׀ sinβ = R, тоді ׀  ׀ = ωR.
׀ = ωR.
Отже, формула Ейлерадоведена.
Продиференціюємо обидві частини рівняння v= R ω, маємо:

або
at=R×e.
Підставивши в формулу 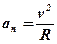 значення швидкості, маємо:
значення швидкості, маємо:
an = Rw2.
Дотичне прискорення  напрямлене по дотичній до траєкторії руху точки в бік руху, якщо тіло обертається прискорено, і в зворотному напрямі, якщо воно обертається сповільнено. Нормальне прискорення
напрямлене по дотичній до траєкторії руху точки в бік руху, якщо тіло обертається прискорено, і в зворотному напрямі, якщо воно обертається сповільнено. Нормальне прискорення  завжди напрямлене по радіусу до осі обертання (рис.6).
завжди напрямлене по радіусу до осі обертання (рис.6).
Повне прискорення точки А:

 Відхилення вектора повного прискорення від радіуса кола, яке описує точка, визначається кутом α, який обчислюється за формулою:
Відхилення вектора повного прискорення від радіуса кола, яке описує точка, визначається кутом α, який обчислюється за формулою:
 або
або 
Через те що в даний момент часу ω і ε для всіх точок обертання тіла мають одне і те ж значення, то із формули випливає, що прискорення всіх точок тіла, яке обертається навколо осі, пропорційні їх відстаням від осі обертання.
Задача. При запуску двигуна його шків діаметром d= 0,2 м протягом перших декількох секунд обертається згідно рівняння φ= 0,2 t3. Визначити швидкості й прискорення точок, розміщених на ободі шківа в момент часу t1 =5 с.
Розв'язання. Диференціюючи рівняння руху шківа, знаходимо його кутову швидкість:
 .
.
У момент часу t1 =5с: w= 0,6×52 = 15 рад/с.
Продиференціювавши рівняння кутової швидкості шківа, визначимо його кутове прискорення:
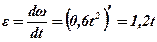 .
.
У момент часу t1=5с: e= 1,2×5 = 6 рад/с2.
Знаходимо швидкість і прискорення точок, розміщених на ободі шківа:
v = w×R = 15×0,1 = 1,5 м/c,
 .
.
Питання для самоконтролю
1. У чому полягають завдання кінематики твердого тіла?
2. Який рух тіла називається поступальним? Його приклади.
3. Сформулювати і довести теорему про траєкторії, швидкості та прискорення точок у поступальному русі тіла.
4. Який рух тіла називається обертальним? Приклади та рівняння обертального руху.
5. Дати означення середній кутовій швидкості, кутовій швидкості в даний момент часу. Як визначається остання?
6. Дати означення середньому кутовому прискоренню, кутовому прискоренню в даний момент часу. Як воно визначається?
7. Записати рівняння рівномірного та рівнозмінного обертання.
8. Як визначається лінійна швидкість точок тіла у його обертальному русі?
9. Довести формулу Ейлера.
10..Як визначається прискорення точок тіла у його обертальному русі?
Лекція № 13
Тема: “Плоскопаралельний рух твердого тіла”
План
1. Рівняння плоскопаралельного руху.
2. Визначення швидкостей та прискорень точок тіла у плоскопаралельному русі.
3. Миттьовий центр швидкостей Теорема про проекції швидкостей двох точок тіла у його плоскопаралельному русі.
Дата публикования: 2015-09-18; Прочитано: 5270 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
