Применение методов векторной алгебры для решения геометрических задач

Пример 11. В равнобедренном треугольнике АВС () точка Е делит боковую сторону в отношении 3:1 (считая от вершины В). Найти угол между векторами и , если

Рис. 3.4

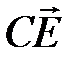Решение. Обозначим угол между векторами и через . Так как 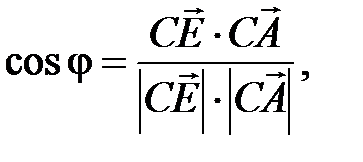для получения ответа надо найти 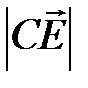и скалярное произведение .

Легко видеть (рис. 3.4), что и что . Поэтому, пользуясь свойствами скалярного произведения, имеем

() = = = = .

Опуская высоту в треугольнике АВС, получаем прямоугольный треугольник , в котором . Тогда =

Поскольку величина угла между векторами и равна , то = . Значит () = 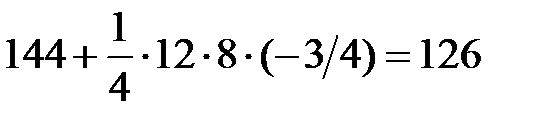. Далее по теореме косинусов имеем

=

=

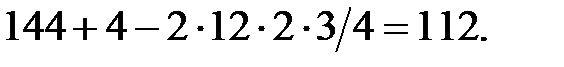
Теперь получаем, что

Значит, .

Ответ: .

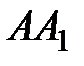Пример 12. Длина ребра куба равна 1. На ребре взята точка Е так, что длина отрезка АЕ равна 1/3. На ребре ВС взята точка F так, что длина отрезка BF равна 1/4. Через центр куба и точки E и F проведена плоскость . Найти расстояние от вершины до плоскости (рис. 3.5).

Рис. 3.5

Решение. Обозначим через ортогональную проекцию точки на плоскость . Введем в пространстве систему координат, поместив начало координат в точку и направив ось Ох по лучу , ось Оy по лучу , ось Cz по лучу и взяв за единицу масштаба отрезок, длина которого равна 1. Тогда точки E, F, K, B ₁ будут иметь следующие координаты: E (1; 0; 1/3), F (0; 1/4; 0); K (1/2; 1/2; 1/2), B ₁(0; 0; 1). Поскольку векторы и не коллинеарны и точка Q лежит в плоскости a, то существyют числа b и g такие, что и . Поскольку 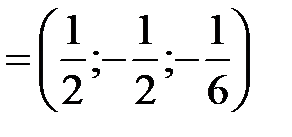, , , то

.

Вектор ортогонален векторам и , поэтому

0 = (, ) =

.

0 = (, )=

.

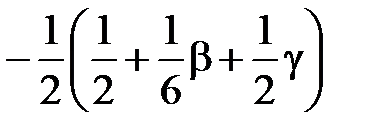
Решая эту систему относительно b и g,

; ,

находим b = –12/85 и g = 18/85. Тогда , и искомое расстояние равно

.

Ответ: .

Пример 13. В основании пирамиды SABC лежит правильный треугольник, а точка O – основание высоты SO пирамиды – является серединой стороны AB и SO = 3:2. На ребрах SC и SB взяты соответствующие точки P и Q – средины этих ребер. Найти угол между прямыми AP и CQ (см. рис. 3.6).

Решение. Соединим точку O с точкой C. Так как SO – высота пирамиды, то SO ^ AB и SO ^ OC. Кроме того, треугольник ABC правильный, поэтому CO ^ AB. Таким образом, удобно выбрать прямоугольную систему координат , как показано на рисунке. Примем сторону основания равной AB = 2. Тогда SO = 3, OC = 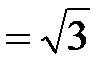. Найдем координаты нужных для дальнейших вычислений точек. Имеем O (0; 0; 0), , A (0; 1; 0), S (0; 0; 3), B (0; –1; 0), , . 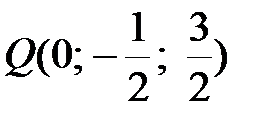Далее находим координаты векторов , . Теперь прямым счетом находим = . Итак, угол между прямыми AP и CQ равен arccos .

Рис. 3.6