 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение типовых задач. Скалярным произведением векторов и называется число
|
|
Скалярным произведением  векторов
векторов  и
и  называется число
называется число

 , (3.14)
, (3.14)
где  – угол между векторами
– угол между векторами  и
и  .
.
Приняты обозначения скалярного произведения  или (
или ( ).
).
Отметим следующие свойства скалярного произведения:
1)  =
= 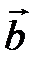
 ; 2)
; 2)  =
=  +
+  ; 3)
; 3)  .
.
В частности: 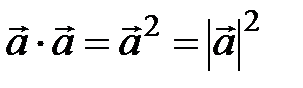 , откуда
, откуда
 . (3.15)
. (3.15)
Скалярное произведение векторов, заданных своими координатами, выражается формулой
 =
=  . (3.16)
. (3.16)
Косинус угла между векторами  и
и  определяется по формуле
определяется по формуле
 . (3.17)
. (3.17)
Необходимое и достаточное условие перпендикулярности векторов  и
и  имеет вид
имеет вид
 или
или  . (3.18)
. (3.18)
Если скалярное произведение отрицательно 
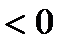 , то угол между векторами
, то угол между векторами  и
и  тупой. Если
тупой. Если 
 , то угол между векторами
, то угол между векторами  и
и  острый.
острый.
Необходимым и достаточным условием коллинеарности ненулевых векторов  и
и  является существование такого числа
является существование такого числа  , что
, что
 . (3.19)
. (3.19)
Если  , то векторы имеют одинаковое направление, если
, то векторы имеют одинаковое направление, если  , то направление противоположное. Из выражения (3.13) следует, что у коллинеарных векторов координаты пропорциональны:
, то направление противоположное. Из выражения (3.13) следует, что у коллинеарных векторов координаты пропорциональны:
 =
=  =
=  .
.
Аппарат векторной алгебры позволяет создать особый метод решения различных геометрических задач. В таблице приводятся примеры использования векторного языка для формулировки и доказательства некоторых геометрических утверждений или вычисления геометрических величин.
| Что требуется (на геометрическом языке) | Что достаточно сделать (на векторном языке) |
1. Установить параллельность прямых  и и 
| Вводятся отрезки 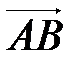 и и  , находят , находят 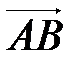  , где отрезки , где отрезки 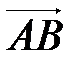 и и  принадлежат соответственно прямым m и n; принадлежат соответственно прямым m и n;  – число – число
|
2. Установить, что точки А, В и С принадлежат прямой 
| Установить справедливость одного из следующих равенств:  , или , или  , или , или 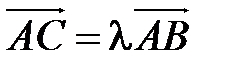 ;
Доказать равенство ;
Доказать равенство
 , где , где  и и  – произвольная точка прямой – произвольная точка прямой
|
3. Установить перпендикулярность прямых m и n (т. е. 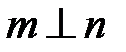 ) )
| Из скалярного произведения  , где точки А и В принадлежат прямой m, а точки , где точки А и В принадлежат прямой m, а точки  и и  – прямой n – прямой n
|
4. Вычислить длину отрезка 
| В некоторой системе координат превратить искомый отрезок АВ в вектор 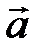 и воспользоваться формулой и воспользоваться формулой 
|
5. Вычислить величину угла 
| Выбрать на сторонах угла векторы  и и  и воспользоваться формулой и воспользоваться формулой  , где , где  – угол между векторами – угол между векторами  и и 
|

| Рис. 3.2 |
 и
и  служат диагоналями параллелограмма
служат диагоналями параллелограмма 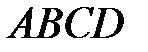 . Выразить
. Выразить  через
через  и
и  (рис. 3.2).
(рис. 3.2).
Решение. По определению суммы и разности векторов имеем  +
+  =
=  ,
, 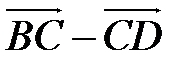 =
=  . Сложив эти равенства, получим
. Сложив эти равенства, получим

 . Далее находим:
. Далее находим:

 ,
,
 ,
, 
Пример 2. Векторы  и
и  служат сторонами треугольника
служат сторонами треугольника  . Найти длину медианы
. Найти длину медианы  .
.
Решение.  =
=  (
(
 ),
),  =
=  =(1; –1; 4).
=(1; –1; 4).
 .
.
Ответ:  .
.
Пример 3. При каком значении  векторы
векторы  и
и  перпендикулярны?
перпендикулярны?
Решение. Воспользуемся формулой (3.17)
 =
=  ,
,  ,
,  .
.
Ответ: 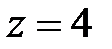 .
.
Пример 4. При каком значении 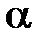 векторы
векторы  и
и  коллинеарны?
коллинеарны?
Решение. Воспользуясь соотношением (3.18), получим  . Отсюда:
. Отсюда:  ,
,  ,
,  . Решая эту систему получим
. Решая эту систему получим 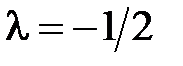 ,
, 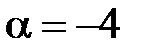 . Или из пропорциональности координат
. Или из пропорциональности координат
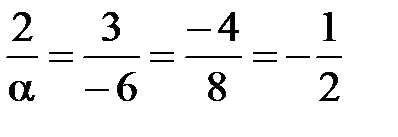
 .
.
Ответ: при  .
.
Пример 5. Даны вершины треугольника  ,
,  ,
,  . Найти
. Найти  .
.
Решение. Находим координаты векторов  ; имеем
; имеем  ,
,  . Угол
. Угол  равен углу между векторами
равен углу между векторами  и
и  , обозначим его через
, обозначим его через 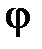 , тогда
, тогда
 =
=  .
.
Ответ: 
 ,
,  .
.
Пример 6. Векторы  и
и  образуют угол равный
образуют угол равный  . Зная, что
. Зная, что  ,
,  вычислить
вычислить
( )(
)( ).
).
Решение. Найдем скалярное произведение
( )(
)( )=
)= 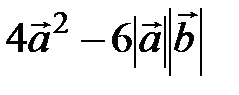
 +
+ 

 =
=
= 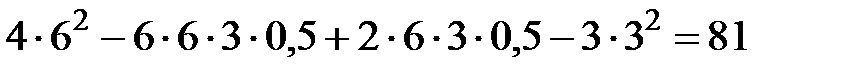 .
.
Ответ: ( )(
)( )
)  .
.
Пример 7. Даны векторы  и
и  , такие, что
, такие, что  ,
,  ,
,  . Найти
. Найти  .
.
Решение. Воспользуемся соотношением (3.15) для нахождения
модуля вектора через скалярное произведение. Находим  =
=  .
.
Аналогично, находим
 =
=
=  .
.
Получаем  =
=  ;
; 
 . Складываем эти два соотношения:
. Складываем эти два соотношения: 

 . Переходим к числам
. Переходим к числам 

 , отсюда
, отсюда 

 , или
, или  . Второе значение корня не удовлетворяет условию задачи.
. Второе значение корня не удовлетворяет условию задачи.
Ответ:  .
.
Пример 8. Найти координаты точки  , лежащей на оси Ох и одинаково удаленной от точек А (1; 2; 3) и В (2; 2; 4).
, лежащей на оси Ох и одинаково удаленной от точек А (1; 2; 3) и В (2; 2; 4).
Решение. Так как точка  лежит на оси Ох, то ее вторая и третья координаты равны нулю, т. е. координаты точки
лежит на оси Ох, то ее вторая и третья координаты равны нулю, т. е. координаты точки  есть
есть 
 . По формуле (2.6) расстояния между двумя точками имеем
. По формуле (2.6) расстояния между двумя точками имеем
 .
.
 .
.
Поскольку  , то
, то 
 .
.
Обе части полученного уравнения определены при всех значениях и неотрицательны. Следовательно, это уравнение равносильно уравнению  , его единственный корень
, его единственный корень  .
.
Ответ: координаты точки  (
( ; 0; 0).
; 0; 0).
Пример 9. В параллелограмме 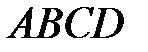 известны координаты вершины
известны координаты вершины  , векторы
, векторы  и
и  . Найти сумму координат вершины А.
. Найти сумму координат вершины А.

| Рис. 3.3 |
Пусть искомые координаты точки А будут  , тогда вектор
, тогда вектор

 . Кроме того,
. Кроме того,  , тогда
, тогда 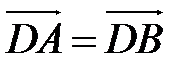 –
–  . Переходя к координатам, будем иметь
. Переходя к координатам, будем иметь

 ;
;

 ;
;

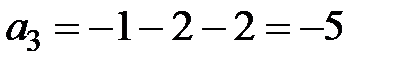 .
.
Суммируя полученные координаты, получаем

Ответ: 
Пример 10. В декартовой прямоугольной системе координат Оху на кривой  заданы две точки А и В. При этом скалярные произведения
заданы две точки А и В. При этом скалярные произведения  и
и  где
где  – единичный вектор оси Ох. Найти вектор
– единичный вектор оси Ох. Найти вектор 
 и его длину.
и его длину.
Решение. Запишем координаты единичного вектора оси Ох, вектора  . Обозначим координаты вектора
. Обозначим координаты вектора 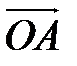 как
как  координаты вектора
координаты вектора  как
как  , тогда наши скалярные произведения, согласно условию задачи:
, тогда наши скалярные произведения, согласно условию задачи:
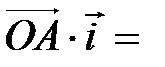
 ;
; 
 .
.
Отсюда получаем  ,
,  . Нам известно, что точки А и В лежат на кривой
. Нам известно, что точки А и В лежат на кривой  , тогда найдем вторые координаты
, тогда найдем вторые координаты 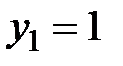 и
и  векторов
векторов 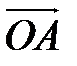 и
и  (координаты этих векторов такие же, как и у точек А и В, поскольку точка О (0; 0). Итак, координаты векторов
(координаты этих векторов такие же, как и у точек А и В, поскольку точка О (0; 0). Итак, координаты векторов 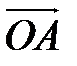
 и
и 
 . Находим вектор
. Находим вектор 

 . Далее находим модуль этого вектора
. Далее находим модуль этого вектора  .
.
Ответ:  .
.
Дата публикования: 2015-09-17; Прочитано: 273 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
