 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Понятие вектора. Прямоугольная декартова система координат
|
|
Элементы векторной алгебры
Теоретические основы темы и решение типовых задач
Понятие вектора. Прямоугольная декартова система координат
Величины, которые характеризуются не только числовым значением, но и направлением, называются векторными.
Отрезок, имеющий определенную длину и определенное направление, называется вектором. О всяком отрезке 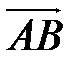 из этого множества говорят, что он представляет вектор
из этого множества говорят, что он представляет вектор 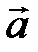 (получен приложением вектора
(получен приложением вектора 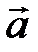 к точке
к точке 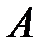 ).
).
Вектор, длина которого равна единице, называется единичным вектором или ортом.
Векторы, параллельные одной и той же прямой, называются коллинеарными. Два вектора называются равными, если они коллинеарны, направлены в одну сторону и имеют одинаковую длину.
Пусть на плоскости задана прямоугольная система координат.
Прямоугольной системой координат на плоскости называется упорядоченная пара двух взаимно перпендикулярных координатных осей Ох и Оу (рис. 3.1). Точка О – начало координат. Векторы 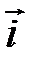 ,
,  – единичные векторы, направленные вдоль осей Ох, Оу соответственно. Они называются базисными векторами прямоугольной системы координат (или ортами).
– единичные векторы, направленные вдоль осей Ох, Оу соответственно. Они называются базисными векторами прямоугольной системы координат (или ортами).
Проекции вектора 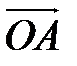 на координатные оси Ох и Оу, обозначим через
на координатные оси Ох и Оу, обозначим через 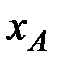 и
и 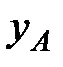 (рис. 3.1). Эти проекции вектора
(рис. 3.1). Эти проекции вектора 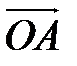 называются его координатами.
называются его координатами.
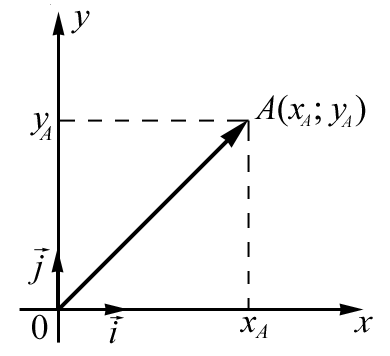
| Рис. 3.1 |
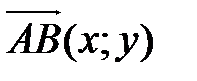 находятся по формулам:
находятся по формулам:
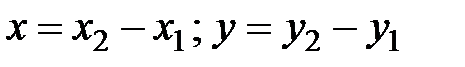 , (3.1)
, (3.1)
где точки А и В имеют координаты соответственно (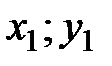 ) и (
) и (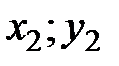 ). Тот факт, что вектор
). Тот факт, что вектор 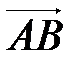 имеет координаты
имеет координаты 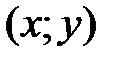 может быть записан так:
может быть записан так:
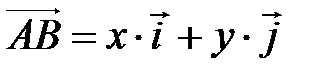 . (3.2)
. (3.2)
Иначе, вектор 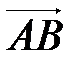 представлен в разложении по базису
представлен в разложении по базису 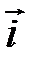 ,
,  .
.
Расстояние между точками плоскости А и В, имеющими координаты соответственно (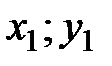 ) и (
) и (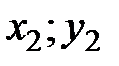 ), определяются по формуле
), определяются по формуле
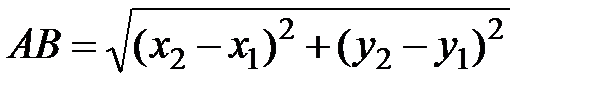 . (3.3)
. (3.3)
По этой же формуле определяется длина отрезка 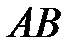 или модуль вектора
или модуль вектора 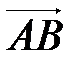 .
.
Координаты (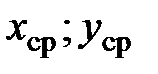 ) средины отрезка
) средины отрезка 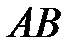 определяются по формулам:
определяются по формулам:
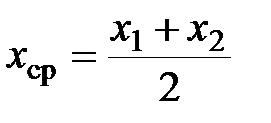 ;
; 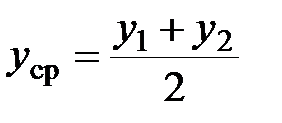 . (3.4)
. (3.4)
Если вектор 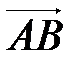 имеет координаты
имеет координаты 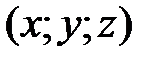 , т. е. задана прямоугольная система координат в пространстве, его можно записать так:
, т. е. задана прямоугольная система координат в пространстве, его можно записать так:
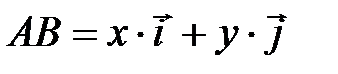
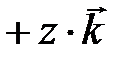 , (3.5)
, (3.5)
т. е вектор представлен в разложении по базису 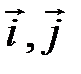
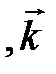 . Векторы
. Векторы 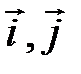
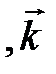 – единичные векторы, направленные вдоль осей Ох, Оу, Оz соответственно.
– единичные векторы, направленные вдоль осей Ох, Оу, Оz соответственно.
Координаты вектора 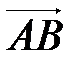
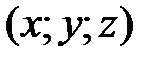 находятся по формулам:
находятся по формулам:
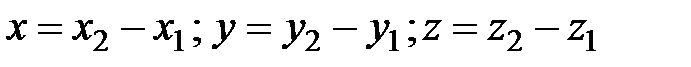 , (3.6)
, (3.6)
где точки А и В, имеют координаты соответственно (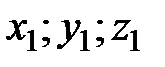 ) и (
) и (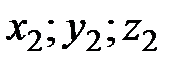 ). Расстояние между точками А и В, имеющими координаты соответственно (
). Расстояние между точками А и В, имеющими координаты соответственно (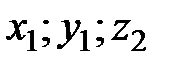 ) и (
) и (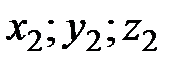 ), определяются по формуле
), определяются по формуле
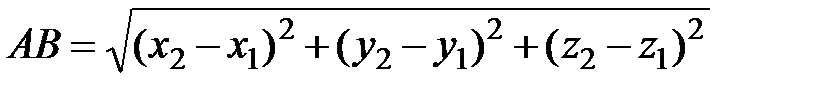 . (3.7)
. (3.7)
По этой же формуле определяется длина отрезка 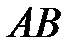 или модуль вектора
или модуль вектора 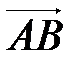 .
.
Координаты (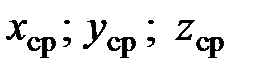 ) средины отрезка
) средины отрезка 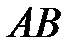 определяются по формулам:
определяются по формулам:
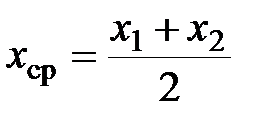 ;
; 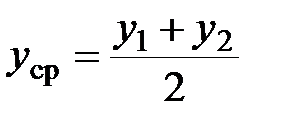 ;
; 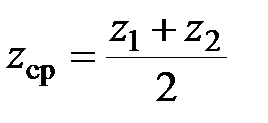 . (3.8)
. (3.8)
В общем случае, модуль вектора 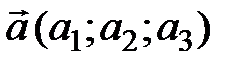 , заданного своими декартовыми координатами, находится по формуле
, заданного своими декартовыми координатами, находится по формуле
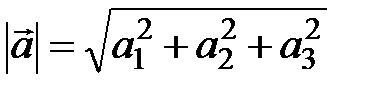 . (3.9)
. (3.9)
Единичный вектор 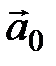 , сонаправленный с вектором
, сонаправленный с вектором 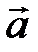 , находится по формуле
, находится по формуле
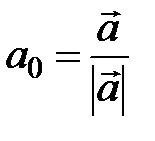 . (3.10)
. (3.10)
Для операций сложения, вычитания и умножения вектора на число справедливы следующие соотношения:
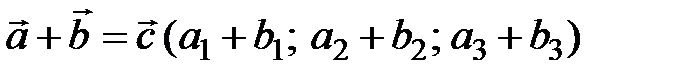 ; (3.11)
; (3.11)
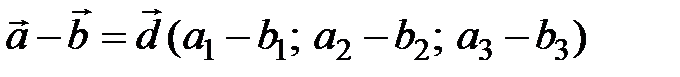 ; (3.12)
; (3.12)
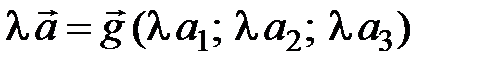 , (3.13)
, (3.13)
где 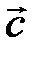 =
= 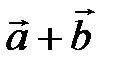 ;
; 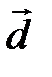 =
= 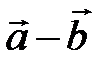 ;
; 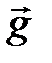 =
= 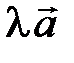 .
.
Дата публикования: 2015-09-17; Прочитано: 399 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
