Способы описания циклических кодов

Циклические коды получили широкое распространение благодаря их эффективности при обнаружении и исправлении ошибок. Схемы кодирующих и декодирующих устройств для этих кодов строятся на основе обычных регистров сдвига.

Циклическим кодом называется линейный блочный (n, m)-код, который характеризуется свойством цикличности, т.е. сдвиг влево на один шаг любого разрешенного кодового слова дает также разрешенное кодовое слово, принадлежащее этому же коду и у которого, множество кодовых слов представляется совокупностью многочленов степени (n -1) и менее, делящихся на некоторый многочлен g (x) степени k = n - m, являющийся сомножителем двучлена xⁿ +1.

Название кода произошло от его свойства, заключающегося в том, что каждая кодовая комбинация может быть получена путем циклической перестановки символов комбинации, принадлежащей этому же коду. Это означает, что если кодовая комбинация а ₀ а ₁ а ₂… а_{n -1} является разрешенной комбинацией циклического кода, то комбинация вида а_{n -1} а ₀ а ₁ а ₂… а_{n -2} так же является разрешенной комбинацией и принадлежит этому коду. Запись а ₀ а ₁… а_{n -1} означает, что кодовая комбинация состоит из n разрядов, первый из которых а ₀, последний а_{n -1}.

Отличие комбинации а_{n -1} а ₀ а ₁ а ₂… а_{n -2} от комбинации а ₀ а ₁ а ₂… а_{n -1} состоит в том, что последний разряд а_{n -1} становится первым, а предпоследний а_{n -2} становится последним. Такая перестановка называется циклической.

Циклические коды часто описываются с использованием многочленов (полиномов) переменной X

X = Р (x); Р (x) = a_{n -1} x^{n -1} + … + a ₁ x + a ₀, (8.63)

где а_i – цифры данной системы исчисления (в двоичной системе 0 и 1). Так, например, двоичное семиразрядное число 1010101 может быть записано в виде полинома:

Р (x) = 1 x ⁶ + 0 x ⁵ + 1 x ⁴ + 0 x ³ + 1 x ² + 0 x ¹ + 1 x ⁰ = x ⁶ + x ⁴ + x ² + 1. (8.64)

То есть цифры двоичного кода рассматриваются как коэффициенты многочлена Р (x). Наибольшая степень х в слагаемом с ненулевым коэффициентом называют степенью многочлена (полинома). Представление кодовых комбинаций в виде (8.63) позволяет свести действия над комбинациями к действиям над многочленами. При этом сложение двоичных многочленов сводится к сложению по модулю 2 коэффициентов при равных степенях переменной х

х^а + х^а = 0; х^а +0 = х^а; 0 + 0 = 0. (8.65)

Умножение производится по обычному правилу перемножения степенных функций:

(8.66)

Рассмотрим пример умножения многочленов

и

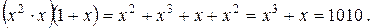
Либо умножение можно произвести следующим образом

1 1 0 1 1

1 1 0 1 1 0

1 0 1 0.

Деление осуществляется по правилу деления степенных функций, при этом операции вычитания заменяются операциями суммирования по модулю 2.

Рассмотрим пример деления многочлена

на бином 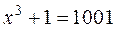. Вначале рассмотрим деление комбинаций.

	1 1 1 0 1 0	1 0 0 1
Å	1 0 0 1		1 1 1	- результат деления –
	0 1 1 1 1 0
Å	1 0 0 1
	0 1 1 0 0
Å	1 0 0 1
	0 1 0 1	- остаток.

А теперь рассмотрим деление полиномов

х 5+ х 4+ х 3+ х

х 3+1

Å

х 5+ х 2

х 2+ х +1

- результат деления – 1 1 1

х 4+ х 2+ х 3+ х

новый многочлен

Å

х 4+ х

х 3+ х 2

новый многочлен

Å

х 3+ 1

х 2+1

- остаток- 0 1 0 1.

Представления комбинаций в форме (8.63) удобно еще тем, что упомянутая ранее циклическая перестановка есть результат простого умножения данного полинома на х. Если одна из кодовых комбинаций выражается полиномом

Р (x) = a ₀ + a ₁ x + a ₂ x ² + a ₃ x ³ + … + a_{n -1} x^{n -1}, (8.67)

то новая комбинация за счет циклического сдвига будет x × Р (x):

x × Р (x) = a ₀ x + a ₁ x ² + a ₂ x ³ + a ₃ x ⁴ + a_{n -2} x^{n -1} + a_{n -1} xⁿ. (8.68)

В последнем члене необходимо заменить хⁿ на х⁰. Новую комбинацию обозначим Р ¹(x)

Р ¹(x) = a_{n -1} х⁰ + a ₀ x + a ₁ x ² + a ₂ x ³ + … + a_{n -2} x^{n -1}. (8.69)

Пример. Рассмотрим, как получить новую комбинацию из кодовой комбинации 1010101= x ⁶ + x ⁴ + x ²+1 путем циклического сдвига. Циклический сдвиг получается умножением многочлена, соответствующего исходной комбинации на х

Р (x) × х = х ×(x ⁶ + x ⁴ + x ²+1) = x ⁷ + х ⁵ + x ³ + x. (8.70)

Заменив х ⁷ на х ⁰ т.е. на «1» получим новую кодовую комбинацию Р ¹(x) в виде полинома:

Р ¹(x) = х ⁵ + x ³ + x + 1. (8.71)

Р ¹(x) соответствует кодовой комбинации 0101011. Таким образом, в результате циклической перестановки исходной кодовой комбинации 1010101 получена новая кодовая комбинация 0101011 также принадлежащая циклическому коду. Заметим, что запись кода в виде многочлена получается более компактной, чем в матричном виде.

Циклический сдвиг на один разряд соответствует алгебраическому умножению некоторого многочлена g (x), который выбран в качестве исходного на х. Процесс получения новых комбинаций кода можно представить следующим образом g (x), х g (x), х ² g (x), х ³ g (x),…, х^{n -1 g} (x).

Многочлен, взятый в качестве исходного, называют образующим или порождающим.

Принцип обнаружения ошибок при помощи циклического кода заключается в том, что в качестве разрешенных принимаются только те комбинации, которые без остатка делятся на заранее выбранный образующий многочлен g (x). Если принимаемая комбинация искажена, то это условие на приемной стороне не будет выполнено. В результате этого формируется сигнал, указывающий на наличие ошибки.

Задача состоит в том, чтобы сформировать кодовые комбинации на передаче, удовлетворяющие указанному условию. Метод построения кодовых комбинаций используется следующий. В процессе кодирования многочлен Р (x) отображающий двоичный код передаваемого сообщения (примитивный код) умножаются на х^k. При этом длина кодовой комбинации увеличивается на k разрядов. Эти дополнительные разряды будут проверочными. Полученное произведение Р (x)× x^k делят на специально подобранный образующий многочлен g (x). При этом получают остаток R (x). Данный остаток R (x) суммируют с произведением Р (x)× x^k. Получают кодовую комбинацию F (x)= Р (x)× x^k + R (x), которая будет без остатка делиться на g (x).

Алгоритм формирования комбинаций циклического кода показан на рис. 8.14.

Покажем справедливость такого способа формирования циклического кода. Обозначим частное от деления Р (x)× x^k на g (x) как f (x). Тогда справедливо равенство Р (x)× x^k = f (x)× g (x) – R (x), где R (x) остаток деления Р (x)× x^k на g (x).

Перенося R (x) за знак равенства получим:

Р (x)× x^k + R (x) = f (x)× g (x).

При таком методе построения коэффициенты при высших степенях являются обозначениями информационных разрядов, а коэффициенты при степенях порядка k -1 и ниже – проверочными.

Рис. 8.14. Алгоритм формирования циклического кода

Рассмотрим использование описанного алгоритма формирования комбинаций циклического кода на примере.

Пример. Требуется закодировать сообщение 1011. Дано: порождающий полином g (x)= х ³+ х ² + 1, общее число разрядов n = 7, число информационных разрядов m =4, число избыточных разрядов k = 3.

Решение:

1. Для кодирования сообщения 1011 определим, какому многочлену оно соответствует: Р (x) = 1× x ³ + 0× x ² + 1× x ¹ + 1× x ⁰ = x ³ + x + 1.

2. Разделим полином Р (x)× x^k на порождающий g (x) для определения остатка R (x):

Р (x)× x^k = Р (x) x ³ = (x ³ + x + 1)× x ³ = x ⁶ + x ⁴ + x ³

	х 6+ х 4+ х 3	х 3+ х 2+1
Å	х 6+ х 5 + х 3		х 3+ х 2
	х 5+ х 4
Å	х 5+ х 4 + х 2
	х 2	- остаток	R (x)= x 2

3. Суммируем произведение Р (x)× x ³ с полученным остатком x ² получим кодовый многочлен F (x)

F (x) = G (x)× x ³ + R (x) = x ⁶+ х ⁴+ х ³ + х ².

В двоичном коде этому многочлену соответствует кодовая комбинация 1011 100. В этой кодовой комбинации последние три позиции занимают проверочные разряды (выделены).

Проверим возможность обнаружения ошибки при приеме кодовой комбинации циклического кода указанным выше алгоритмом. Пусть принимается рассмотренная выше комбинация F (x)=1011100. Порождающий полином должен быть известен на приеме. Вынесение решения о наличии ошибки основывается на анализе остатка R (x) от деления комбинации на порождающий полином g (x) если R (x) = 0, то ошибки нет.

Кодовой комбинации 1011100 соответствует многочлен F (x)= x ⁶+ x ⁴+ x ³+ х ².

Делим F (x) на g (x)

	х 6+ х 4+ х 3+ х 2	х 3+ х 2+1
Å	х 6+ х 5 + х 3		х 3+ х 2
	х 5+ х 4+ х 2
Å	х 5+ х 4 + х 2

Остаток R (x)=0, следовательно, ошибки нет.

Допустим, в результате воздействия помех в канале связи вместо комбинации 1011100 принято 0011100. Этой комбинации соответствует многочлен х⁴+х³+х². Деление на g (x) дает:

	х 4+ х 3+ х 2	х 3+ х 2+1
Å	х 4+ х 3 +х		х
	х 2+ х		Остаток R (x) ¹0

Ошибка обнаружена.

Возможно применение циклического кода в качестве кода с исправлением ошибок. В этом случае на приеме получают остаток от деления принятой комбинации кода на порождающий многочлен. Места искаженных разрядов определяются путем анализа остатка.