Обертання

Розглянемо плоский трикутник АВС.

Рис. Обертання і відображення

Здійснимо поворот на 90° проти годинникової стрілки. В результаті отримаємо трикутник А*В*С*

Поворот на 180°задається матрицею для А**В**С**

Поворот на 270° навколо початку координат - за допомогою такої матриці для А***В***С***:

4. Зміна масштабу

Зміна масштабу визначається значенням 2-х елементів головної діагоналі матриці.

Якщо використовуємо матрицю,, маємо збільшення в 2 рази.

Якщо значення діагональних елементів не рівні, то має місце спотворення.

o Трикутник АВС перетворений за допомогою матриці

o Трикутник DEF перетворений за допомогою матриці

Рівномірна і нерівномірна зміни масштабу трикутників АВС та DEF

5. Тривимірні перетворення

Наочне представлення об'єкта можна одержати шляхом виконання операцій:

· обертання;

· переносу;

· побудови проекцій.

Точка в тривимірному просторі

• (x y z) задається чотиримірним вектором (x y z 1) чи (X Y Z H).

Перетворення з однорідних координат описується співвідношеннями

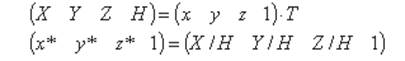
де T - деяка матриця перетворення.

6. Тривимірні обертання

При обертанні навколо осі х розміри уздовж осі х не змінюються.

Таким чином, матриця перетворень буде мати нулі в першому рядку і першому стовпці, за винятком одиниці на головнійдіагоналі.

Обертання навколо осі y

Для обертання на кут Ф навколо осі y - нулі ставлять у другому рядку і другому стовпці матриці перетворення, за винятком одиниці на головній діагоналі. Повна матриця задається виразом

Обертання навколо осі z

Аналогічно матриця перетворення для обертання на кут φ навколо осі z має вигляд

Стандартні проекції.

План лекції

1. Афінна і перспективна геометрія

2. Проекції

1.

2.

2.1. Аксонометрична проекція

2.2. Тривимірні проекції

2.3. Плоска геометрична проекція

2.3.1. Центральна проекція

2.3.2. Паралельна проекція

2.4. Рівнобіжні проекції

2.4.1. Ортографічні проекції

2.4.2. Косокутні проекції

2.5. Ізометрична проекція

1. Афінна і перспективна геометрія

важливим поняттям, що характеризує дану геометрію - паралельність і співвідношення між паралельними прямими.

Афінне перетворення

• є комбінацією лінійних перетворень, супроводжуваних переносом зображень.

• останній стовпець в узагальненій матриці перетворення розміром 4×4 повинен бути рівним

(0 0 0 1).

Перспективне перетворення

• у перспективній геометрії немає двох прямих, паралельних одна одній, і перспективна площина може бути розглянута як напівсферична поверхня;

• перспективне перетворення має місце у випадку, коли останній стовпчик узагальненої матриці перетворення 4×4 не нульовий.

2. Проекції

• перетворення точки, заданої в системі координат розмірністю n, у точку системи координат розмірністю, меншою ніж n.

Види проекцій

• Перспективна проекція являє собою перетворення зображення з тривимірного простору в двовимірний;

• Аксонометрична проекція – це перспективна проекція, у якій центр проектування розташовується в нескінченності.

Вид проекції залежить від розташування центра проектування.

Застосування проекцій

• Перспективними зображеннями часто користуються художники й архітектори, тому що ці зображення дозволяють одержати картину, близьку до реальної.

• Аксонометричні зображення в свою чергу використовують конструктори.

Аксонометрична проекція

• утворюється за допомогою афінного перетворення.

• Існують кілька типів аксонометричних проекцій, що застосовуються в нариснійгеометрії й інженерній графіці

• для одержання математичних залежностей, що описують аксонометричні проекції, використовується матриця перетворення розміром 4×4.

• точки проектуються на площину з центра проектування в нескінченності.

Тривимірні проекції

• Коли об'єкт (представлений у виді сукупності точок) будується за допомогою прямих проектуючих променів, що називаються проекторами, які виходять з центра проекції, проходять через кожну точку об'єкта і, перетинаючи картинну площину, утворюють проекцію.

Плоска геометрична проекція

• проектування в цьому випадку здійснюється на площину, а не на викривлену поверхню і як проектори використовуються прямі а не криві лінії.

Класи плоскої геометричної проекції

• Центральні проекції

– якщо відстань між центром проекції і проекційною площиною обмежена,

– її центр проекції є явним.

• Паралельні проекції

– якщо відстань між центром проекції і проекційною площиною нескінченна,

– центр проекції нескінченно віддалений і всі проектори паралельні.

Відрізок АВ і його центральна проекція А'В‘

Відрізок АВ і його паралельна проекція А'В‘

Центральна проекція

• використовується у випадках, коли бажано досягти певного ступеня реальності.

• це досягається за допомогою перспективного скорочення - розмір центральної проекції об'єкта змінюється обернено пропорційно до відстані від центра проекції до об'єкта.

• із проекції не можна одержати інформацію про відстані:

– кути зберігаються тільки на тих гранях об'єкта, що паралельні проекційній площині;

– проекції паралельних прямих у загальному випадку не паралельні.

Паралельна проекція

• породжує менш реалістичне зображення,

• оскільки відсутнє перспективне скорочення, хоча при цьому можуть мати місце різні постійні скорочення вздовж кожної з осей.

• Проекція фіксує дійсні розміри:

– паралельні прямі залишаються паралельними.

– кути зберігаються тільки на тих гранях об'єкта, що паралельні проекційній площині.

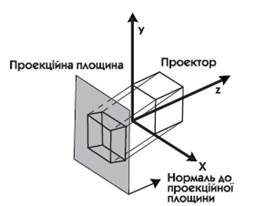
Рівнобіжні проекції

поділяються на два типи в залежності від співвідношення між напрямком проектування і нормаллю до проекційної площини:

• ортографічних паралельних проекціях ці напрямки збігаються, напрям проектування є нормаллю до проекційної площини

• косокутних паралельних проекціях вони не збігаються.

Ортографічні проекції

Види ортографічних проекцій

– вид зверху (план)

– вид збоку,

у яких картинна площина перпендикулярна головним координатним осям.

Побудова трьох ортографічних проекцій

Косокутні проекції

• другий тип паралельних проекцій

• має властивості ортографічних проекцій (видів спереду, зверху і збоку)

• можна вимірювати кути і відстані.

• Проектування інших сторін об'єкта також допускає проведення лінійних вимірів (але не кутових) уздовж головних осей.

• нормаль до проекційної площини і напрям проектування не збігаються.

Види косокутних проекцій

• Кавальє (cavalier);

• Кабіне (cabinet).

Ізометрична проекція

• у цьому випадку нормаль до проекційної площини (а, отже, і напрямок проектування) утворює n- ні кути з кожною з головних координатних осей.

Властивість ізометричної проекції

• усі три головні координатні осі однаково зменшуються. Тому можна проводити виміри вздовж напрямків осей з тим самим масштабом

• головні координатні осі проектуються так, що їхні проекції утворюють між собою рівні кути.

Представлення точок і зображень у Растровій графіці.

План лекції

1. Креслення відрізків

1.1. Покроковий алгоритм

1.2. Покрокові методи

1.2.1. Креслення кіл

2. Заповнення (заливка)

2.1. Алгоритми заповнення

3. Відсікання

3.1. Алгоритми відсікання

3.2. Двовимірні алгоритми відсікання

1. Креслення відрізків

Розкладанням у растр називається процес визначення пікселів, як найкраще апроксимуючих заданий відрізок.

Розкладання в растр відрізків прямих

Загальні вимоги до алгоритмів креслення відрізків

• відрізки повинні виглядати прямими, починатися і закінчуватися в заданих точках,

• яскравість уздовж відрізка повинна бути постійною і не залежати від довжини і нахилу,

• малювати потрібно швидко.