Випереджена нормальна форма

Означення 7.1. Випереджена нормальна форма – формула, записана у вигляді Q₁x₁Q₂x₂...Q_nx_nM, де кожне Q_ix_i (i = 1,2,..., n) – це " x_i або $ x_i, а формула M не містить кванторів. Вираз Q₁x₁...Q_nx_n називають префіксом, а M – матрицею формули, записаної у випередженій нормальній формі.

Приклад 7.1. Наведемо приклади формул, записаних у випередженій нормальній формі.

1. " x " y (P (x,y)Ù Q (y)).

2. " x $ y (P (x)Ú Q (y)).

3. " x " y $ z (Q (x,y)Ù R (z)).

4. " x " y " z $ u (P (x,z)Ú P (y,z)Ú Q (x,y,u)). ▲

Для того, щоб перевести формулу у випереджену нормальну форму, необхідно виконати наступні перетворення:

1. Використати правила усунення імплікації (P®Q = 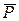Ú Q) та еквівалентності (P~Q =(P®Q)Ù(Q®P)).

2. Застосувати закон подвійного заперечення (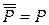) та закони де Моргана ().

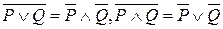3. Застосувати закони: Ø(" xP (x))= 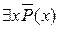та Ø($ xP (x))= .

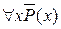4. Застосувати закони логіки першого ступеня 3-8.

5. Винести квантори у префікс, для чого скористатись законами логіки першого ступеня 3-8.

Приклад 7.2. Зведемо формулу " xP (x)→$ уQ (y) до випередженої нормальної форми за умови, що предикати P (x) і Q (y) не містять вільних змінних. Кроки для побудови випередженої нормальної форми:

1. Вилучення імплікації:

" xP (x)→$ уQ (y)= Ø(" xP (x))Ú$ уQ (y).

2. Застосування закону Ø(" xP (x))= :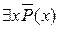

Ø(" xP (x))Ú$ уQ (y)= 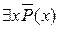))Ú$ уQ (y).

3. Винесення квантора існування у префікс:

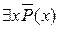))Ú$ уQ (y) =$ х $ у ( 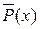Ú Q (y)). ▲

Приклад 7.3. Зведемо формулу " x " y ($ zP (x,z)Ù P (y,z))® $ uQ (x,y,u)) до випередженої нормальної форми. Кроки для побудови випередженої нормальної форми:

1. Вилучення імплікації:

" x " y ($ zP (x,z)Ù P (y,z))® $ uQ (x,y,u))= " x " y (Ø($ zP (x,z)Ù P (y,z)))Ú$ uQ (x,y,u)).

2. Застосування закону Ø(" xP (x))= 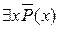та закону де Моргана:

" x " y (Ø($ zP (x,z)Ù P (y,z)))Ú$ uQ (x,y,u))= " x " y (" z 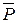(x,z)Ú 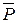(y,z))Ú$ uQ (x,y,u)).

3. Використання законів логіки першого ступеня 6-7 та винесення квантора існування у префікс:

" x " y (" z 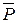(x,z)Ú 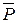(y,z))Ú$ uQ (x,y,u))= " x " y " z $ u ( 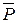(x,z)Ú 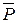(y,z)Ú$ uQ (x,y,u)). ▲