Решение. Проверим на абсолютную сходимость

Проверим на абсолютную сходимость. Рассмотрим ряд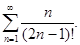

Применим признак Даламбера, для этого нужно найти отношение последующего члена к предыдущему.

следовательно ряд сходится, значит соответствующий положительный ряд сходится, следовательно исходный ряд сходится абсолютно.

Замечание к теореме Лейбница.

При замене суммы знакочередующегося ряда на его частичную сумму S_n (S ≈ S_n) погрешность приближения не превзойдет первого отброшенного члена u_{n +1}.

R_n – знакочередующийся ряд, следовательно 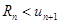(по теореме Лейбница).

пример. Вычислить с точностью α = 0,001 сумму ряда