Решение. Знакочередующиеся ряды исследуем по теореме Лейбница

Знакочередующиеся ряды исследуем по теореме Лейбница.

1)

значит начиная с 100 числа условие теоремы выполняется., поэтому отбросим первые 99 членов, что не повлияет на сходимость.

2)

Значит по теореме Лейбница ряд сходится.

Исследуем на абсолютную сходимость.

Рассмотрим ряд

Поэтому применим предельную форму признака сравнения, в качестве v_n выберем ряд

значит ряды v_n и u_n ведут себя одинаково.

А ряд расходится (как обобщенно-гармонический 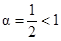), то следова­тельно ряд тоже расходится.

Ряд сходится условно.

пример. Исследовать на абсолютную и условную сходимость ряд