 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Метод касательных
|
|
(метод Ньютона)
Метод касательных, связанный с именем Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Предположим, что функция f(x), имеющая корень с на отрезке [a, b], дифференцируема на этом отрезке, и ее производная f`(x) не обращается на нем в нуль. Возьмем произвольную точку xo и напишем в ней уравнение касательной к графику функции f(x):
y = f(xo)+f`(xo)(x-xo).
График функции f(x) и ее касательной близки около точки касания, поэтому естественно ожидать, что точка x1 пересечения касательной с осью x будет расположена недалеко от корня с (рис. 5).
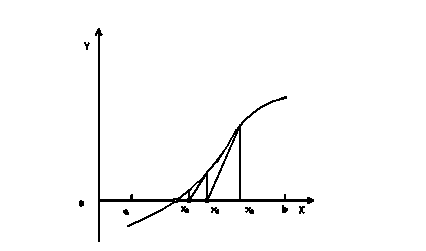
Рис. 5. Построение последовательности по методу касательных
Для определения точки x1 имеем уравнение
f(x o ) + f `(x o )(x 1 -x o )=0.
Таким образом,
x 1 = x o - f(x o )/f `(x o ).
Повторим проделанную процедуру: напишем уравнение касательной к графику функции f(x) при x = x 1 и найдем для нее точку пересечения x2 с осью x (рис. 5):
x 2 = x 1 - f( x1 )/f `(x 1 ).
Продолжая этот процесс, получим последовательность {xn}, определенную с помощью рекуррентной формулы:
xn+ 1 =xn - f(xn)/f `(xn), n= 0, 1, 2 ,...
При исследовании этой последовательности, как и последовательности метода итераций, встают два вопроса:
1. Можно ли процесс вычисления чисел xn продолжать неограниченно, т.е. будут ли числа xn принадлежать отрезку [a, b]?
2. Если итерационный процесс бесконечен, то как ведет себя последовательность {xn} при n→ ∞?
Дата публикования: 2015-07-22; Прочитано: 232 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
