 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Линии второго порядка
|
|
Лекция 12
Эллипс: определение,каноническое уравнение, свойства.
Df: Эллипсом называется множество точек плоскости для каждой из которой сумма расстояний до 2-х фиксированных точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
F1,F2 - 2 различные точки (фокусы)
| F1F2| = 2c
j = {M| | F1M| + | F2M | = 2Q}, где Q > с (2)
Составим уравнение эллипса. Для этого ведем на плоскости ДПСК R = {O, (i, j)}|
O – середина [F1F2], i F1F2, j | R – правый репер
 (3)
(3)
Пусть "M(x,y) Î j Þ | F1M | + | F2M | = 2 Q
j:  (4) –уравнение эллипса
(4) –уравнение эллипса
Преобразуем уравнение (4). Для этого возведем обе части уравнения в квадрат.
( )2 = (2Q
)2 = (2Q  )2
)2
x2 + 2xc + c2 + y2 = 4a2 + 4a 
a2 – cx = a 
Возведем в квадрат
(a2 – cx)2 = (a  )2
)2
a4 – 2a2cx + c2x2 = a2x2 – 2a2cx + a2c2 + a2y2
(a2 - c2)x2 + a2y = a2(a2 - c2)
(2) Þ a2 - c2 > 0, поэтому обозначим: b2 = a2 – c2 (5)
b2x2 + a2y2 = a2b2

 (6)
(6)
Уравнение (6), полученное из уравнения (1) путем 2-х кратного возведения в квадрат, это следствие уравнения (1), т.е. j Í j* (7)
Покажем, что j* Í j
"M(x,y)Î j* Þ y2 = (b2(1  )) (8)
)) (8)
Найдем расстояние от т.М до фокусов:

= 
= 
r1 = | a +  |; r2 = | a -
|; r2 = | a -  | (9)
| (9)
Аналогично найдем r2 = | F2M |

= 
= 
Раскроем модуль: (8) Þ 1 
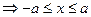 (10)
(10)
(2), (10)  (11)
(11)
(9), (10)  (12)
(12)
| F1M | + | F2M | = r1 + r2 = a + 

Отсюда следует, что  Þ j* Í j (13)
Þ j* Í j (13)
(7), (13) Þ j* = о - эллипс
Уравнение (6) – уравнение эллипса
 - каноническое уравнение эллипса
- каноническое уравнение эллипса
Df: Отрезок, соединяющий фокус с произвольной точкой эллипса, называется
фокальным радиусом.
Формулы (12) позволяют вычислить величину фокальных радиусов, зная абсциссу точки, определяющий фокальный радиус
E =  (14) – эксцентриситет эллипса, он показывает меру сплющенности
(14) – эксцентриситет эллипса, он показывает меру сплющенности
(2), (14) Þ E < 1
Свойства эллипса.
R = {O, (i, j)}, j = {M(x,y) |  }
}
Используя это уравнение, найдем свойства эллипса.
10. эллипс имеет 2 оси симметрии, которые совпадают с осями координат и центр симметрии, который совпадает с началом координат.
Следуем из того, что в каноническом уравнении x и y входят только в четных степенях, поэтому M(x,y) Î о Þ
Þ (M’(-x,y) Î j, M’’(-x,-y) Î j, M’’’(x,-y) Î j)
20. все точки эллипса лежат внутри прямоугольника со сторонами 2a, 2b, стороны которого параллельны осям координат и центр совпадает с началом координат, т.е. эллипс ограниченная линия.
Доказательство:
(6) 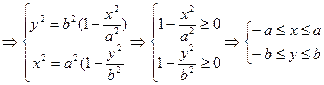
30. Эллипс выпуклая кривая.
Это означает, что эллипс ограничивает на плоскости выпуклую область, любые 2 точки которой можно соединить отрезком, целиком, лежащим в этой области.
Для доказательства этого свойства воспользуемся следующим признаком выпуклости кривой: ограниченная кривая на плоскости выпукла Û когда она с любой прямой плоскости пересекается не более чем в 2-х точках
"e: Ax + By + c = 0
j  e:
e: 

Последняя система координат содержит одно уравнение 1-ой степени, второе 2-ой степени, очевидно,что система имеет 2 решения.
Учитывая симметрии эллипса, выявленные св. 10,дальнейшее исследование эллипса достаточно проводить в I четверти.

Когда x возрастает от 0 до а, y – убывает от b до 0. Полученные свойства позволяют изобразить эллипс. Точки пересечения эллипса с осями координат называются вершинами эллипса, их четыре: A1(-a,0) Î Ox B1(0,-b) Î Oy
A2(a,0) Î Ox B2(0,b) Î Oy
Отрезки осей к-т, заключенные между вершинами эллипса называются осями эллипса.
 - оси эллипса
- оси эллипса
(5) Þ b<a при любых a и b;
b – малая ось
a – большая ось.
Фокусы эллипса лежат на большой оси.
Эллипс как результат сжатия окружности.
Возьмем W(0, r = a):
x2 + y2 = a2
Подвергнем плоскость сжатию к оси Ox


 где b2 = k2a2
где b2 = k2a2
Параметрические уравнения эллипса.
Пусть дан эллипс j; M(x,y) Î j
M1 = [OM2]ÇW1
M2 = [OM1]ÇW2
t = (Ox^,OM1)
M1’= OxÇM1M1’^Ox
M = M1M2’ÇM2M || Ox
M(x,y)
DOM1M1’Þ x = acos t (1)
M2= OxÇM2M2’^Ox
DOM2M2’Þ y = bsin t (2)
 (3)
(3)
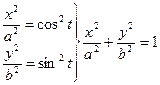
Лекция 13
Гипербола: определение, каноническое уравнение, свойства, асимптоты.
Df: Гиперболой называется множество точек плоскости для каждой из которых абсолютная величина разности расстояния до 2-х фиксированных точек плоскости, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
F1, F2 – фокусы | F1 F2 | = 2c (1)
Абсолютная величина разности | D | = 2a (1)
j = { M || F1M |-| F2M | = 2o,a < с }
a<c (3)
Введем на плоскости R = {O, (i, j)} | O – середина [F1 F2]
i F1 F2; j | R – правый репер F1(-c,o) (4)
В этой СК фокусы имеют координаты: F2(-c,o)
"M(x,y) Î j Û ||F1M|-|F2M|| = 2a
|F1M|-|F2M| = ± 2a
|F1M| = ±2a + |F2M|
Заменим последнее уравнение в координатах:
 (5) – уравнение гиперболы, но в плохом виде.
(5) – уравнение гиперболы, но в плохом виде.
Преобразуем уравнение (5), возведя его в квадрат:



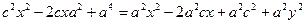
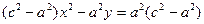
(3) Þ с2 – a2 > 0 b2 = c2 – a2 (6)
b2x2 – a2y2 = a2b2 Þ  (7)
(7)
Уравнение (7) получено путем двукратного возведения в квадрат уравнения гиперболы (5), следовательно является следствием уравнения (5). Тогда все точки уравнения (5) входят в состав уравнения (7). Покажем, что верно и обратное включение, т.е. что всякая точка j* принадлежит гиперболе, т.е. j Í j* (8)
"M(x,y) Î j* Þ y2 = b2(x2/a2 – 1) (9)
Найдем расстояние от точки M до фокусов:


 (10)
(10)


 (11)
(11)
Объединим формулы (10) и (11) в систему:
 (12)
(12)
Найдем знаки выражений, стоящих под знаком абсолютной величины
(9) 
Рассмотрим каждый случай отдельно:
1).  /*c / a
/*c / a


 (13)
(13)

 (14)
(14)
(13), (14) ® (12): x 
 (15) – фокальные радиусы левой ветви.
(15) – фокальные радиусы левой ветви.
2). 

 (16)
(16)  (17)
(17)


 (18) - фокальные радиусы правой ветви.
(18) - фокальные радиусы правой ветви.
1). (15) Þ || F1M | - | F2M || = | r1 – r2| = |  = | -2a | = 2a
= | -2a | = 2a
2). || F1M | - | F2M || = | r1 – r2| = |  = | 2a | = 2a
= | 2a | = 2a
Т.о. доказано, что "M Î j* принадлежит гиперболе, т.е. j*Î j (19)
(8), (9) Þ j*Î j. Следовательно (7) – уравнение гиперболы.
 - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.
Точки, абсциссы которых  называют точками левой ветви гиперболы. Точки, абсциссы которых
называют точками левой ветви гиперболы. Точки, абсциссы которых  называют точками правой ветви гиперболы.
называют точками правой ветви гиперболы.
Расстояние от точки гиперболы до ее фокуса называют фокальным радиусом точки.
Тогда из сказанного следует, что формулы (15), определяют фокальные радиусы левой ветви, а формулы (18) – правой ветви.
E =  - эксцентриситет гиперболы
- эксцентриситет гиперболы
Т.к. с > 0, то Е > 1
Используя эксцентриситет формулы (15),(18) можно переписать в виде:



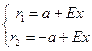
Дата публикования: 2015-07-22; Прочитано: 390 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
