Пучок прямых

Df: Пучком прямых называют множество всех прямых пересекающихся в одной точке.

Общая точка всех прямых пучка называется центром пучка.

Если S – центр пучка, то пучок прямых обозначается:

{S} = {e | S Î у}

Составим уравнение пучка прямых. Для этого выберем на плоскости афинную СК R = {O, (e₁, e₂)}

Рассмотрим 2 случая:

1). Центр пучка задан

S – центр пучка; S(x₀, y₀)

" e: y = kx + b (1)

S(x₀, y₀) Î e Þ y₀ = kx₀ + b (2)

(1) – (2): {S}: y – y₀ = k(x – x₀); - ¥ < k< +¥

y – y₀ = k(x – x₀) – уравнение пучка

Введя условный коэффициент 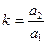; a (a₁, a₂) || e

a₂(x-x₀) – a₁(y-y₀) = 0

2). Центр пучка не задан

e₁: A₁x + B₁y + c₁ = 0 (3)

e₂: A₂x + B₂y + c₂ = 0 (4)

(5)

S = e₁ Ç e₂

{S}: p(A₁x + B₁y + c₁) + q(A₂x + B₂y + c₂) = 0 (6), где p и q – независимо друг от друга пробегают все действит. числа не обращаются в ноль одновременно.

1. Докажем, что (6) – уравнение прямой линии.

Доказательство:

(pA₁ + qA₂)x + (pB₁ + qB₂)y + (pc₁ + qc₂) = 0

Показываем, что это уравнение не первой степени.

Предположим противное, т.е. ,что противоречит условию (5)

Уравнение (6) задает прямую линию.

2. Покажем, что координаты т. S удовлетворяют уравнению (6)

S(x,y) = e₁ Ç e₂ Þ (8)

(6),(8) ® p

3. Покажем, что уравнение (6) задает любую прямую пучка

M₁(x₁,y₁)ÏS

Подставим коэффициенты т.М в уравнение (6)

p(A₁x₁+B₁y₁+c₁)+q(A₂x₁+B₂y₁+c₂) = 0

; (9)

При этих значениях параметра, получим прямую, т.е. из

(9), (6) Þ (A₂x₁+B₂y₁+c₂)(A₁x+B₁y+c₁)+(A₁x₁+B₁y₁+c₁)(A₂x+B₂y+c₂) = 0 (10)

Последнее доказывает, что уравнение (6) задает все параметры пучка.

Лекция 11.

Основные метрические задачи прямой.

Задача № 1

Угол между двумя прямыми.

Df: Угол между 2-мя прямыми называется угол между их направляющими векторами.

Из Df Þ что угол определяется в точностью до смежного.

R = {O, (i, j)} a₁(B₁, -A₁) || e₁

e₁: A₁x + B₁y + c₁ = 0 (1) a₂(B₂, -A₂) || e₂

e₂: A₂x + B₂y + c₂ = 0 (2) j = (e₁, ^ e₂) = (a₁, ^ a₂)

j = (e₁, ^ e₂) cos =

———————————

Найти: j -?

cos = (3)

(3) Þ e₁ ^ e₂ Û A₁A₂ + B₁B₂ = 0 (4)

e₁ || e₂ Û (4)

Пусть прямые e₁ || e₂ заданы уравнениями с условными коэффициентами, т.е.

e₁: y = k₁x + b₁ (5)

e₂: y = k₂x + b₂ (6)

Обозначим j = (e₁, ^ e₂), j₁ = (o_x ^ e₁), j₁ = (o_x ^ e₂)

(все углы ориентированны)

j₂ = j + j₁

j = j₂ - j₁

tgj = tg(j₂ - j₁) =

Учитывая, что tgj₁ = k₁, tgj₂ = k₂:

(7)

Из (7) Þ e₁ || e₂ Û tgj = 0 Û k₁= k₂

(7)Þe₁ ^ e₂ Û tgj - не $ Û 1 + k₁k₂ = 0 Û

Û k₂ = -

e₁ || e₂ Û k₁ = k₂

e₁ ^ e₂ Û k₂ = -1/ k₁

Задача № 2

Расстояние от точки до прямой.

R = {O, (i, j)}

e: xcosa+ysina - p = 0 (1)

M₀(x₀,y₀) Ï e

————————————

Найти: r(M₀, e) = d -?

Проведем через т.М₀ прямую e^* || e

e^* | M₀ Î e^*, e^* || e, и составим ее нормальное уравнение

(2)

e^*: xcosa + ysina - (p ± d) = 0

M₀(x₀, y₀) Î e^* Þ x₀cosa + y₀sina - (p ±d) = 0

d = ± (x₀cosa + y₀sina) – p

Т.к. d ³ 0 Þ d = | x₀cosa + y₀sina - p | (3)

Правило: чтобы найти расстояние от точки до прямой достаточно в левую часть нормального уравнения подставить координаты точки и взять абсолютную величину полученного числа.

R = {O, (i, j)}

e: Ax + By + с = 0 (4)

Для того чтобы воспользоваться правилом вычисления расстояния от точки до прямой надо привести уравнение (4) к нормальному виду. Для этого умножим обе части уравнения на нормирующий множитель N.

NAx + NBy + Nc = 0 (5)

Учитывая соотношения, которым удовлетворяют коэффициенты нормального уравнения, получим:

(NA)² + (NB)² = 1

(6)

Из (5), (6) Þ

(7)

Воспользовавшись правилом, получим:

d = 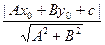(8)

Пример: вычислить расстояние от т.М (4, 3) до прямой e: x – 2y + 6 = 0. В заданной

ДПСК.

R = {O, (i, j)} d = =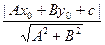

M (4,3) =

e: x – 2y + 6 = 0

————————

d = r (M, e) -?