Примеры построения различных видов аппроксимирующих функций

Пусть функция задана таблицей 3.1. Требуется построить методом наименьших квадратов функцию, приближающую табличную наилучшим образом. Для удобства обозначений изменим нумерацию исходных данных и будем считать, что ; ; ; ; 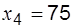; ; ; ; 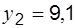. Сделаем предположение относительно характера аппроксимирующуей функции, рассмотрев расположение точек, заданных таблицей, на графике (рис. 1.).

По характеру расположения точек на графике можно выдвинуть предположение о линейной квадратичной или показательной зависимости величин. Рассмотрим все три предположения.

Случай 1. Будем искать приближающую функцию в виде линейной функции .

Сумма мер отклонений 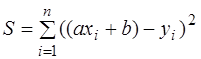, где ; - число измерений. Найдём неизвестные коэффициенты из системы:

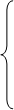
После преобразования система принимает вид:

… (1)

Составим вспомогательную таблицу

Таблица 6.1.

		9,1		227,5
		8,7
		5,6
		2,5
		35,9		1332,5

Подставив данные из таблицы 6.1 в систему (1), получим:

откуда , а уравнение линейной функции

.

Случай 2. Аппроксимирующая функция – квадратичная.

Сумма мер отклонений . Неизвестные коэффициенты будут найдены из системы:

,

преобразовав которую, получим:

… (2)

Составим вспомогательную таблицу.

Таблица 6.2

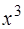
					9,1	227,5	5687,5
					8,7
					5,6
					2,5
					35,9	1332,5	83937,5

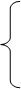Подставим данные из таблицы 6.2 в систему (2):

и, решив её, получим значения параметров:

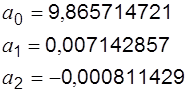
Уравнение квадратичной зависимости:

Случай 3. Найдем приближающую функцию в виде показательного выражения . После логарифмирования показательной функции

и введения обозначений ; ; , функция записывается как линейная .

Построим таблицу соответствия известных значений:

Таблица 6.3

			2,30
		9,1	2,20
		8,7	2,16
		5,6	1,72
		2,5	0,92
		35,9	9,3

Запишем систему:

Подставим данные из таблицы 6.3 в систему (3):

и получим в результате:

Возвращаясь к показательной функции, запишем:

; ; .

Значения линейной функции: ;

Квадратичной функции:

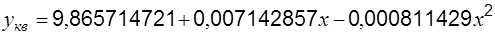
Показательной функции:

и их отклонения от табличных значений функции в заданных точках сведём в таблицу 6.4

Таблица 6.4

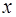
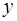
		9,1	8,7	5,6	2,5
	0,88	-0,07	-1,52	-0,27	0,98
	-0,13	0,44	-0,51	0,24	-0,03
	2,28	-0,22	-2,28	-0,95	0,86

На основании таблицы 6.4 вычисляется сумма квадратов отклонений аппроксимации для каждого из трёх рассмотренных видов приближения:

Следовательно, для заданной табличной функции наиболее целесообразна квадратичная аппроксимация.

По полученным результатам строятся графики.