Нахождение неизвестных параметров в случае задания эмпирической формулы в виде многочлена или показательной функции

Пусть в качестве аппроксимирующей функции выбран многочлен степени :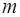

Тогда сумма квадратов отклонений примет вид:

,

а неизвестные параметры будут определяться системой уравнений:

Если приближающая функция выбрана в виде показательной функции , то выражение можно светсти к линейному, логарифмируя левую и правую части равенства:

или .

После введения обозначений: 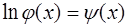, ; , функция записывается как линейная по аргументу :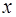

Сумма отклонений определяется формулой:

,

а коэффициенты и находятся из решения системы:

после чего осуществляется обратный переход к параметрам и .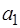

Аналогично можно поступать и в тех случаях, когда в качестве аппроксимирующей функции выбраны, например, гипербола или логарифмическая функция .