Уравнения Колмогорова

Пусть система может находиться в одном из состояний и в случайные моменты времени t переходит из одного состояния в другое с помощью пуассоновского потока событий интенсивностью из в . Заданы начальные вероятности состояний и потоки , переводящие систему из одного состояния в другое. Граф состояний (для определенности – три состояния ) представлен на рис. 3.

Рис. 3

Задача 1. Найти вероятности состояний

Задача 2. Найти предельные вероятности состояний

Решение задачи 1 дается системой дифференциальных уравнений Колмогорова. Число уравнений равно числу состояний.

Правило составления уравнений Колмогорова.

Производная вероятности каждого состояния по t равна сумме всех потоков вероятности, втекающих в данное состояние, минус сумма потоков вероятности, вытекающих из данного состояния, где поток вероятности перехода 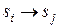– величина .

(7)

Начальные условия:

Если потоки стационарны (), всегда существуют предельные вероятности. Для их нахождения в систему (7) подставим:

Уравнения Колмогорова для предельных вероятностей:

Правило составления: Сумма всех потоков вероятности, втекающих в данные состояния, равна сумме всех потоков вероятности, вытекающих из состояния.