Дискретные цепи Маркова

Рассмотрим некоторую физическую систему S, множество возможных состояний системы конечное или счетное, в системе протекает дискретный марковский процесс. Переходы между состояниями возможны только в фиксированные моменты времени . Указанные переходы можно рассматривать как последовательные шаги процесса: в начальный момент система была в состоянии , на 1 шаге перешла в состояние и т. д. Такие марковские процессы называют дискретными цепями Маркова.

Для цепи Маркова задача 1 о нахождении вероятностей состояний формулируется так:

Найти – вероятность того, что после k- го шага система окажется в состоянии . Будем рассматривать простые цепи Маркова, для которых вероятности 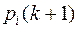зависят только от состояния системы на предыдущем, k- мшаге.

Простая цепь Маркова полностью определяется заданием начальных вероятностей состояний и вероятностей перехода – так называемых условных вероятностей:

Если система была на предыдущем (k – 1) -м шаге в состоянии , то на k-м шаге она перешла в состояние .

Определение 4. Цепь Маркова называется однородной, если вероятности перехода не зависят от номера шага: 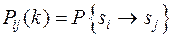, т.е.

Для простоты рассмотрим однородную цепь Маркова. Будем считать, что число состояний системы равно п. Вероятности перехода объединяются в квадратную матрицу .

Сумма вероятностей по всем путям, выходящим из данного состояния, равна 1 (как сумма вероятностей полной группы несовместных событий).

Рассмотрим пример системы с тремя состояниями и матрицей перехода:

(3)

Элемент – вероятность перехода системы из состояния в .Сумма элементов каждой строки равна 1.

Пусть, например, заданы начальные вероятности: 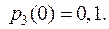Найдем вероятности состояний после 1 шага.

Решение. По формуле полной вероятности:

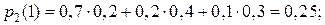
Проверка: 0,23 + 0,25 + 0,52 = 1.

Правило: чтобы найти вектор-строку вероятностей , нужно строку начальных вероятностей умножить на i-й столбец матрицы перехода по правилу умножения матриц.

Аналогично находятся вероятности состояний после любого шага. Полученное правило равносильно следующей формуле:

(4)

Заметим, что в случае неоднородной цепи Маркова вероятности зависят от номера шага.

Рассмотрим однородную цепь Маркова с матрицей вероятностей переходов за один шаг.

Справедлива

Теорема. Матрица вероятностей переходов однородной цепи Маркова за шагов равна ой степени матрицы вероятностей переходов за один шаг, т.е. .

Если известна матрица вероятностей переходов за один шаг и начальные распределения вероятностей состояний , то вероятности состояний на – ом шаге удовлетворяют соотношению

.