Ряды с положительными членами. Признаки сходимости

Определить сходимость ряда (1.1) и найти его сумму в случае сходимости непосредственно по определению 1.1 как предела последовательности частичных сумм, весьма затруднительно. Поэтому существуют достаточные признаки определения сходится ряд или расходится. В случае его сходимости приближенным значением его суммы с любой степенью точности может служить сумма соответствующего числа первых n членов ряда.

Здесь будем рассматривать ряды (1.1) с положительными (неотрицательными) членами, т. е. ряды, для которых Такие ряды будем называть положительными рядами.

Теорема 3.1. (признак сравнения)

Пусть даны два положительных ряда

, (3.1)

, (3.2)

и выполняются условия для всех n=1,2,…

Тогда: 1) из сходимости ряда (3.2) следует сходимость ряда (3.1);

2) из расходимости ряда (3.1) следует расходимость ряда (3.2).

Доказательство. 1. Пусть ряд (3.2) сходится и его сумма равна В. Последовательность частичных сумм ряда (3.1) является неубывающей ограниченной сверху числом В, т. е.

Тогда в силу свойств таких последовательностей следует, что она имеет конечный предел, т. е. ряд (3.1) сходится.

2. Пусть ряд (3.1) расходится. Тогда, если ряд (3.2) сходится, то в силу доказанного выше пункта 1 сходился бы и исходный ряд, что противоречит нашему условию. Следовательно ряд (3.2) также расходится.

Этот признак удобно применять к определению сходимости рядов, сравнивая их с рядами, сходимость которых уже известна.

Пример 3.1. Исследовать на сходимость ряд

Члены ряда положительны и меньше соответствующих членов сходящегося ряда геометрической прогрессии

т. к. , n=1,2,…

Следовательно, по признаку сравнения исходный ряд также сходится.

Пример 3.2. Исследовать на сходимость ряд

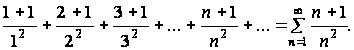
Члены данного ряда положительны и больше соответствующих членов расходящегося гармонического ряда

т. к.

Следовательно, по признаку сравнения исходный ряд расходится.

Теорема 3.2. (Предельный признак Даламбера).

Пусть члены положительного ряда (1.1) таковы, что существует предел

Тогда: 1) при q < 1 ряд (1.1) сходится;

2) при q > 1 ряд (1.1) расходится;

3) при q = 1 о сходимости ряда (1.1) ничего сказать нельзя, необходимы дополнительные исследования.

Замечание: Ряд (1.1) будет расходиться и в том случае, когда

Пример 3.3. Исследовать на сходимость ряд

.

Применим предельный признак Даламбера.

В нашем случае .

Тогда

Следовательно, исходный ряд сходится.

Пример 3.4. Исследовать на сходимость ряд

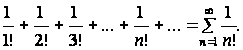
Применим предельный признак Даламбера:

Следовательно, исходный ряд сходится.

Пример 3.5. Исследовать на сходимость ряд

Применим предельный признак Даламбера:

Следовательно, исходный ряд расходится.

Замечание. Применение предельного признака Даламбера к гармоническому ряду не дает ответа о сходимости этого ряда, т. к. для этого ряда

Теорема 3.3. (Предельный признак Коши*).

Пусть члены положительного ряда (1.1) таковы, что существует предел

Тогда: 1) при q < 1 ряд (1.1) сходится;

2) при q > 1 ряд (1.1) расходится;

3) при q = 1 о сходимости ряда (1.1) ничего сказать нельзя, необходимы дополнительные исследования.

Пример 3.6. Исследовать на сходимость ряд

Применим предельный признак Коши:

Следовательно, исходный ряд сходится.

Теорема 3.4. (Интегральный признак Коши).

Пусть функция f(x) непрерывная неотрицательная невозрастающая функция на промежутке

Тогда ряд и несобственный интеграл сходятся или расходятся одновременно.

Пример 3.7. Исследовать на сходимость гармонический ряд

Применим интегральный признак Коши.

В нашем случае функция удовлетворяет условию теоремы 3.4. Исследуем на сходимость несобственный интеграл

Имеем .

Несобственный интеграл расходится, следовательно, исходный гармонический ряд расходится также.

Пример 3.8. Исследовать на сходимость обобщенный гармонический ряд

Функция удовлетворяет условию теоремы 3.4.

Исследуем на сходимость несобственный интеграл

Рассмотрим следующие случаи:

1) пусть Тогда обобщенный гармонический ряд есть гармонический ряд, который расходится, как показано в примере 3.7.

2) пусть Тогда

Несобственный интеграл расходится, и, следовательно, ряд расходится;

3) пусть Тогда

Несобственный интеграл сходится, и, следовательно, ряд сходится.

Окончательно имеем