Скалярное произведение в-ров

Опр: Скалярным произв-м в-ров 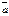и 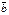наз-ся число, равное произведению их длин на косинус угла между ними.

Скалярным произв-м в-ров 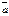и 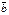обозн-ся через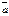 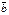. Итак по определению

Теор: (О св-х скалярного произведения). Скалярное произведение в-ров обладает свойствами:

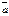1) Пусть и 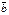- ненулевые в-ры. Тогда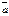 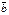=0 .

2) , где наз-ся скалярным квадратом в-ра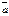

3) =

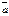
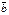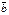
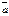
5)

6)

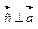О. Векторным произвед. и наз-ся вектор , который удовлетворяет услов.: 1) . 2) и 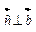. 3) векторы , и - правая тройка.

О. Тройка векторов в пространстве наз-ся правой, если (считая векторы имеющими общее начало) с конца третьего вектора мы видим кратчайший поворот от первого вектора ко второму направленным против часовой стрелки. В противном случае тройка наз-ся левой.

О. Базис наз-ся ортонормированным, если его векторы попарно ортогональны и по длине равны единице. Декартова система координат, базис которой ортонормирован, называется декартовой прямоугольной системой координат.

Св-ва векторного произвед.: 1) геом. смысл: модуль вект. произведения равен площади парал-ма, построенного на вект.-сомножителях. Док-во. Пусть 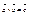. Рассм. ABCD–парал-м, , .

= = . 2) вект. произведение коллинеарных векторов равно нулевому вектору(и обратно:если векторное произвед.ненулевых векторов равно нулевому вектору, то векторы коллинеарны) 3) АнтиКМ . 4) АС относительно скалярного множителя: . 5) АС относительно слож.: = 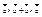. 6) если в ортонормированном базисе , то = = - + = - + .

О. Смешанным произведением трех вект. наз. число, равное скалярному произведению одного из них на вект. произведение двух др.: = = = .

Св-ва смеш. произвед.: 1) геом. смысл: модуль смеш. произвед. равен объему параллелипипеда, построенного на данных вект.. 2) смеш. произвед. вект. равно нулю т. и т. т., к. хотя бы один из вект. нулевой, или хотя бы два вект. коллинеарны, или вект. компланарны. 3) смеш. произвед. не изменяется при круговой перестановке вект.: = = . Д-во. = = = = = = . 4) смешанное проивед. изменяет знак на противополож. при перестановке соседних векторов: = 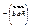5) АС относит. слож.: = = . 6) АС относит. скалярного множителя: = .7)если , , в произвольном базисе, то = ∙ = ∙ - ∙ +

+ ∙

В приложениях математики часто рассматриваются величины, изображаемые векторами: силы, скорости, моменты сил и т. д. Скалярное произвед. используется для док-ва теорем (например, т.Стюарта:пусть АВС-треуг. и D т.на стороне АВ.Тогда ).Векторное произвед. применяется для нах-ия площадей параллелограмма, треугольника. Смешанное произвед. для нах-ия объемов параллелепипеда, тетраэдра.

(к билету №9) Найти решение уравнения , удовлетв. условиям ,

Решение: