Вычитание в-ров

Опр: Разность в-ров 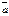и 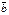наз-ся такой в-р , что .

Разность в-ров обозначается так: -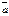

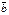
Т: Разность в-ров сущ-т и ед-на.

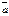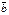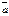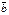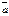Д-во: сущ-е. Отложим данные в-ры и от точки O: и рассм-м в-р . По св-ву треуг-ка и получаем . Значит, по опр-ю в-р является разностью - в-ров и .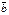

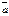Единст-ть. Пусть построены две разности в-ров и 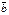. Тогда по опр-ю разности и 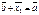. Получим

Применим свойства 1, 4 и 3 сложения в-ров к обоим рав-м. Так как

то 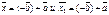. Следовательно,

Умн-ие в-ра на число

Опр: Произведением в-ра 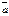на действ-е число α наз-ся в-р, обозн-й α 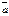кот-й удовлетворяет условиям:

1) ,

2) , если α ≥0 и , если α < 0.

Теор: (Условие коллин-ти в-ров). В-ры и 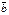коллинеарны ↔ когда сущ-т такое число α, что

Теор: (Св-ва). Произв-х чисел α, β и в-ров 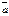, 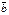справедливы рав-ва:

1)

2)

3)

4)