Фазовые переходы в нефти, воде и газе

Фазовые переходы подчиняются определённым закономерностям, в основе которых лежит понятие равновесия фаз. Равновесие фаз характеризуется константой равновесия, которая зависит от температуры и давления.

Константа фазового равновесия i -го компонента характеризуется отношением мольной доли компонента в газовой фазе (у_i или N_yi) к мольной доле этого компонента в жидкой фазе (х_i или N_xi), находящейся в равновесном состоянии с газовой фазой:

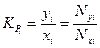. (4.1)

Для определения равновесного состояния газожидкостных смесей используются законы Дальтона и Рауля.

Согласно закону Дальтона каждый компонент, входящий в газовую фазу имеет своё парциальное давление P_i, а общее давление в газовой системе равно сумме парциальных давлений:

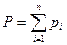. (4.2)

Согласно закону Рауля, парциальное давление компонента над жидкостью (нефтью) равно давлению насыщенного пара (Р_{нас. пара}) или упругости пара (Q_i) этого компонента, умноженному на его мольную долю в нефти:

или 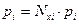, (4.3)

где Q_i – упругость паров компонента;

N_xi – мольная доля компонента;

p_{i нас. пара} – давление насыщенного пара i-го компонента.

В момент равновесия парциальное давление i-го компонента в газовой фазе равно парциальному давлению компонента над жидкостью. И это равновесное состояние двухфазной системы (газовой и нефтяной фаз) описывается законом Дальтона-Рауля:

; (4.4)

Уравнения (4.4), описывающее равновесное состояние двухфазной системы позволяет рассчитать состав равновесной газовой фазы для известного состава жидкой фазы и наоборот – найти равновесный состав жидкой фазы для известного состава газовой фазы и находящейся с ней в контакте.

Воспользуемся соотношением (4.4) и рассчитаем мольные доли компонентов газовой фазы:

Уравнение:

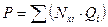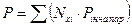или (4.5)

называется уравнением начала однократного (контактного) испарения. Оно характеризует давление, при котором кипит смесь при данной температуре. Температура учитывается в этом уравнении в неявном виде, так как упругости паров (давление насыщенных паров) компонентов зависят от температуры.

Уравнение:

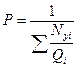(4.6)

называется уравнением конца однократного испарения или уравнением начала однократной конденсации. Оно характеризует величину упругости паров (давления насыщенных паров) углеводородной смеси при данной температуре, при которой кипит смесь при данной температуре.

Уравнения равновесия (4.4), начала однократного испарения (4.5), начала конденсации (4.6) описывают поведение простых углеводородных смесей при низких давлениях и температурах. Для практических промысловых расчетов использовать их затруднительно, так как они не учитывают влияние давления и состава смеси на величину давления паров углеводородов, находящихся в смеси. Поэтому, для практических расчетов используют не упругости паров углеводородов (давления паров), взятые в чистом виде, а константы равновесия, характеризующие отношение:

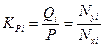, (4.7)

где К_i – константа равновесия i-го компонента при данной температуре и давлении смеси.

Оценить состав газовой (N_yi) и жидкой (N_xi) фаз можно на основе уравнения материального баланса, записанного для одного моля нефтегазовой смеси (N_zi):

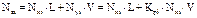, (4.8)

где L – мольная доля жидкой фазы;

V – мольная доля паровой фазы;

N_zi – мольные доли компонентов в нефтегазовой смеси.

Так как ∑ (N_zi) = 1, то сумма мольной доли жидкой фазы (L) и мольной доли паровой фазы (V) равна: V + L = 1. Отсюда следует:

V=1 – L. (4.9)

Используя уравнения (4.8) и (4.9) получим выражение для оценки мольной доли компонента жидкой фазы:

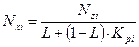, (4.10)

или

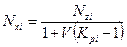, (4.11)

и для оценки мольной доли компонента газовой фазы:

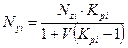. (4.12)

Величины: V и L оцениваются и уточняются методом последовательных проб и приближений.

Уравнение (4.8) при наличии достоверных данных о константах фазовых равновесий углеводородов при различных условиях существования смесей имеет широкое прикладное значение в практике разработки месторождений, нефтедобычи, подготовки скважинной продукции и в нефтепереработке.