Смачивание и краевой угол

Смачиванием называется совокупность явлений на границе соприкосновения трёх фаз, одна из которых обычно является твёрдым телом и две другие – не смешиваемые жидкости или жидкость и газ.

Капля жидкости может растекаться по поверхности, если поверхность хорошо смачивается, а если поверхность плохо смачивается, то капля растекаться не будет.

Интенсивность смачивания характеризуется величиной краевого угла смачивания θ, образованного поверхностью твёрдого тела с касательной, проведённой к поверхности жидкости из точки её соприкосновения с поверхностью (рис. 18).

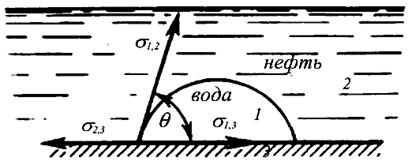
Рис. 18. Форма капли, обусловленная поверхностными натяжениями на различных границах соприкасающихся фаз

Краевой угол θ измеряется в сторону более полярной фазы (в данном случае в сторону воды). Принято условно обозначать цифрой 1 водную фазу, цифрой 2 – углеводородную жидкость или газ, цифрой 3 – твёрдое тело.

Предполагая, что краевой угол  отвечает термодинамическому равновесию, получим уравнение, впервые выведенное Юнгом:

σ _2,3 = σ _1,3 + σ _1,2 cosθ, (6.4)

откуда получим выражение для краевого угла θ:

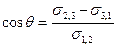= В (6.5)

Если σ _2,3 > σ _1,3, то 0 < cosθ < 1, из чего следует, что угол θ – острый (наступающий), а поверхность – гидрофильная. Если

σ_2,3 > σ _1,3, то –1 < cosθ < 0, из чего следует, что угол θ – тупой (отступающий), а поверхность – гидрофобная.

Существуют также переходные поверхности (амфотерные), которые хорошо смачиваются как полярными, так и неполярными системами.

К гидрофильным поверхностям относятся силикаты, карбонаты, окислы железа. К гидрофобным поверхностям – парафины, жиры, воск, чистые металлы.

Краевой угол смачивания зависит от строения поверхности, адсорбции жидкостей и газов, наличия ПАВ, температуры, давления, электрического заряда.