Параметры трещинной среды

Коллекторские свойства трещинных горных пород характеризуются густотой и раскрытостью трещин, которые определяют трещинную пористость и проницаемость, обусловленную наличием в породе трещин.

Трещиноватость - отношение объёма трещин V_т ко всему объёму V трещинной среды.

. (1.14)

Коэффициент густоты трещин a равен отношению суммарной протяженности трещин к поверхности фильтрации

(1.15)

где а – суммарная протяженность трещин; F – площадь фильтрации.

Трещинная пористость m_т (ее иногда по аналогии с коэффициентом пористости обычных коллекторов называют коэффициентом трещиноватости) определяется отношением объема трещин к объему образца породы:

, (1.16)

где b – раскрытие трещины.

Для трещинно-пористой среды вводят суммарную (общую) пористость, прибавляя к трещиноватости пористость блоков.

Из (1.16) следует, что для идеализированной трещинной среды

m_т= a _тαb_т, (1.17)

где b_т - раскрытость; a _т - безразмерный коэффициент, равный 1,2, 3 для одномерного, плоского и пространственного случаев, соответственно.

Для реальных пород значение коэффициента a зависит от геометрии систем трещин в породе.

Для квадратной сетки трещин (плоский случай) α_т=1 / l_т, где l_т - размер блока породы. Средняя длина трещин l^* равняется среднему размеру блока породы и равна

l^*=1 / α_т. (1.18)

Трещинный пласт - деформируемая среда. В первом приближении можно считать

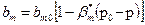, (1.19)

где b_т0 - ширина трещины при начальном давлении р₀; b^* _т =b _п l / b_т0 - сжимаемость трещины; b _п - сжимаемость материалов блоков; l - среднее расстояние между трещинами. Для трещинных сред l / b_т >100.

Проницаемость трещиноватых сред равна

(1.20)

Для трещиновато-пористой среды общая проницаемость определяется как сумма межзерновой и трещинной проницаемостей.