Матрица линейного оператора

В силу теоремы 5.4 линейный оператор в конечномерном линейном пространстве однозначно можно задать при помощи образов базисных векторов. Наряду с ядром, образом, дефектом и рангом для линейного оператора имеет место такая характеристика, как матрица этого оператора.

Пусть 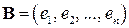– базис в конечномерном линейном пространстве (). Тогда по теореме 5.4 для любых векторов существует единственный линейный оператор 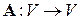, переводящий векторы базиса 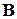в соответствующие векторы , что можно записать в виде следующей операторной системы:

Разложим векторы через векторы базиса :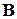

где – некоторые числа.

Определение 5.6. Квадратная матрица

,

столбцами которой являются координатные вектор-столбцы векторов в базисе 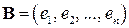, называется матрицей линейного оператора 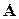в базисе .

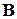Следующая теорема позволяет найти координаты образа в базисе через матрицу оператора и координаты прообраза в том же базисе.

Теорема 5.7. Пусть линейный оператор, действующий в линейном пространстве и базис в . Тогда вектор-столбец координат вектора равен произведению

(5.1)

матрицы оператора в данном базисе на вектор-столбец координат вектора 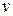в данном базисе.

□ Пусть в базисе 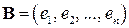линейный оператор имеет матрицу . Разложим векторы через базисные векторы

Учитывая, что образы 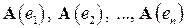базисных векторов базиса 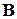имеют разложения

,

получим

В силу того, что разложение вектора по базису 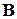единственно, получим

что равносильно матричному равенству (5.1). ■